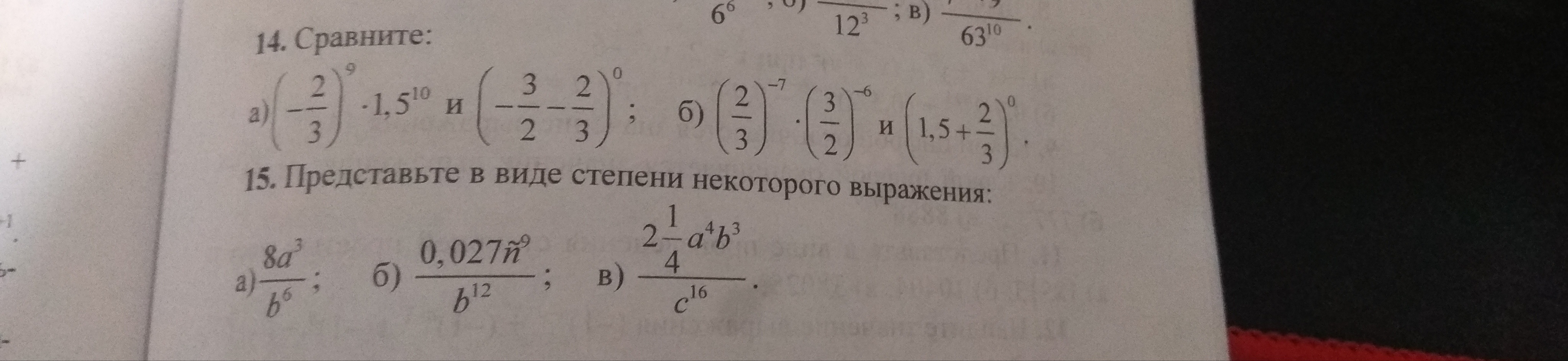Помогите с 2 заданиями на степени

Приложения:

Ответы

Ответ дал: Хуqожнuк

14. а) Левая часть меньше нуля, а правая равна 1, поэтому знак меньше. Привожу и классическое решение:

Левая часть:

$(-frac{3}{2} )^9*1,5^{10} = -frac{3^9}{2^9} *frac{3^{10}}{2^{10}} = -frac{3^{19}}{2^{19}}$

Правая часть:

$a^0=1, aneq0\ (-frac{2}{3}-frac{2}{3}) ^0= (-frac{4}{3}) ^0=1$

Итог:

$-frac{3^{19}}{2^{19}} < 1\\ (-frac{3}{2} )^9*1,5^{10} < (-frac{2}{3}-frac{2}{3}) ^0$

14. б) Левая часть:

$(frac{2}{3})^{-7}*(frac{3}{2}) ^{-6}= (frac{3}{2})^{7}*(frac{2}{3}) ^{6}=frac{3^7}{2^7}*frac{2^6}{3^6}=frac{3}{2}=1,5$

Правая часть:

$(1,5+frac{2}{3})^0=1$

Итог:

$1,5>1 \\ (frac{2}{3})^{-7}*(frac{3}{2}) ^{-6}> (1,5+frac{2}{3})^0$

15.

$a)frac{8a^3}{b^6} = (frac{2a}{b^2} )^3 \ \b) frac{0,027n^9}{b^12} =(frac{0,3n^3}{b^4} )^3\\ c) frac{2frac{1}{4}a^4b^3}{c^{16}} =frac{frac{9}{4}a^4b^3}{c^{16}} = (frac{frac{3}{2}a^2b^{frac{3}{2}}}{c^{8}}) ^2$

Похожие вопросы

Қазақ тiлi

2 года назад

ПЕРЕВЕДИТЕ НА КАЗАХСКИЙ компьютер может стать как другом и помощником, так и врагом - все зависит как от того,как с ним работать.за компьютером можно интересно провести время : играя в игры,получая

Русский язык

2 года назад

Подскажите пожалуйста слова с орфограммой вечер, блузка, сердце, касса.

Математика

2 года назад

срочно помогите плиз

История

2 года назад

Если бы Александра II не убили и курс его внутренней политики был бы про- должен, то какими преобразованиями он бы характеризовался? Каковы могли быть последствия такого курса для России? помогите!!

История

8 лет назад

Николай второй получил прозвище "Кровавый" после: А)Кровавого воскресенья Б) Ходынской трагедии С) Расстрела рабочих на Ленских рудниках

Литература

8 лет назад

Краткое содержание "Каштанка" 1 - 3 предложения

Биология

9 лет назад

Рассмотрите рисунок. К какому типу относятся изображенные на нём ткани? Охарактеризуйте особенности строения и функции этого типа тканей.

Литература

9 лет назад

тема и идея произведения белый бим черное ухо