Диагональ трапеции перпендикулярна и равна одной из ее боковых сторон. Вычислите площадь трапеции, если основания равны 14 и 3
Ответы
Ответ дал:
0
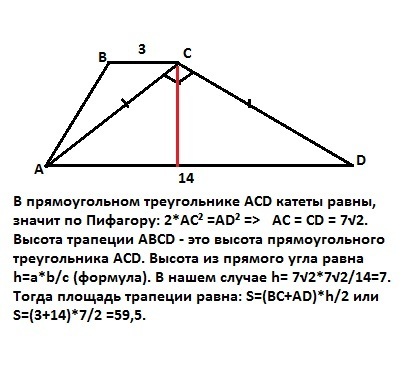
В прямоугольном треугольнике ACD катеты равны, значит по Пифагору: 2*АС² =AD² => AC = CD = 7√2.
Высота трапеции АВСD - это высота прямоугольного треугольника ACD. Высота из прямого угла равна h=a*b/c (формула). В нашем случае h= 7√2*7√2/14=7.
Тогда площадь трапеции равна: S=(BC+AD)*h/2 или
S=(3+14)*7/2 =59,5.
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад