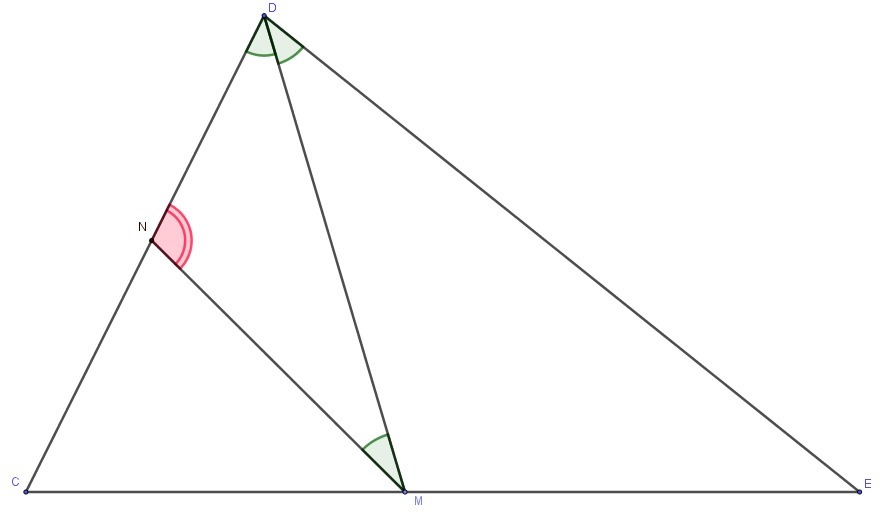
< >

Відрізок DМ − бісектриса трикутника СDЕ. Через точку М проведено пряму, яка паралельна стороні DE і перетинає сторону DС у точці N. Знайдіть кути трикутника DMN, якщо кут CDE дорівнює 68

Ответы

Ответ дал: Аноним
0

Биссектриса делит угол пополам, то есть: tt angle CDM=angle EDM=dfrac{angle CDE}{2}=dfrac{68^circ}{2}=34^circ

tt angle DMN=angle MDE=34^circ как накрест лежащие при MN || DE и секущей DM.


Сумма углов треугольника равна 180°, значит

tt angle DNM=180^circ-angle MDN-angle DMN=180^circ-34^circ-34^circ=112^circ



Ответ: 34°; 34°; 112°.

Приложения:
Похожие вопросы
Русский язык
2 года назад
сочинение на тему почему надо уважать старших.
Русский язык
2 года назад
1.Определите предложение, в котором НЕ со словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. 1 вариант (Не) полученная вовремя телеграмма заставила нас изменить планы. М. Врубель
Математика
2 года назад
Соедини стрелками значения масс в порядке их увеличения. 55 кг 1040 кг 1250 кг 505 кг 1т 1 ц 1 кг 50 ц 50 кг помогите пожалуйста​
Химия
2 года назад
Виберіть правильне твердження. Молярна маса – це: А) відношення кількості речовини до її маси; Б) маса1 моль речовини; В) маса будь-якої кількості речовини; Г)маса 2 моль речовини.
География
8 лет назад
Что такое картодиаграмма?
Математика
8 лет назад
сорока белобока колликцинирует всякие блестящие щтучки она ппринесла в гнездо 4осколказеркала монет принесла в 4 раза больше чем осколков и на 4 больше чем бусин . сколько всего блестящих щтучек в
Математика
9 лет назад
Один із множників дорівнює 26. Як зміниться добуток, якщо інший множник збільшити на 3
Литература
9 лет назад
основные занятия Алеши Поповича