Предмет: Геометрия
Автор: glebovaanan
Вопрос задан 7 лет назад

Основание пирамиды - ромб с большей диагональю d и острым углом альфа. Все двугранные углы при основании пирамиды равны бета. Найдите площадь боковой поверхности пирамиды.

Ответы

Ответ дал: Аноним

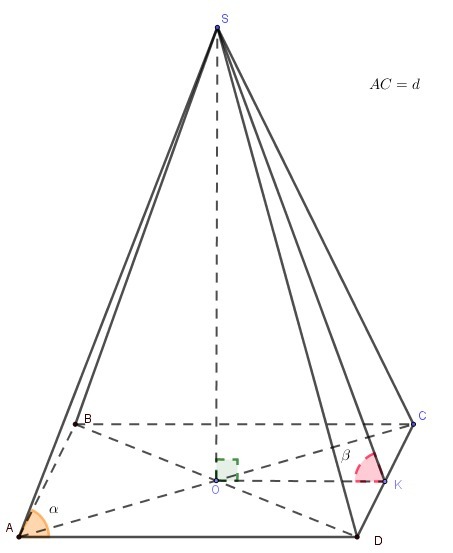
Пусть AC - большая диагональ ромба; AC = d и острый угол $tt angle BAD=alpha$ . Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.

$tt AO=OC=dfrac{AC}{2}=dfrac{d}{2};~~~angle BAO=angle OAD=dfrac{alpha}{2}$

Из прямоугольного треугольника AOD: $tt cos angle OAD=dfrac{OA}{AD}$ отсюда выразим AD: $tt AD=dfrac{OA}{cos angle OAD}=dfrac{d}{2cosfrac{alpha}{2}}=dfrac{d}{2cosfrac{alpha}{2}}$

Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.

$tt h=ADcdotsinalpha=dfrac{dsinalpha}{2cosfrac{alpha}{2}}$ - высота ромба.

Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен $tt r=OK=dfrac{h}{2}=dfrac{dsinalpha}{4cosfrac{alpha}{2}}$

Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды: $tt cos beta=dfrac{OK}{SK}~~Rightarrow~~~ SK=dfrac{OK}{cos beta}=dfrac{dsinalpha}{4cosfrac{alpha}{2}cosbeta}$

Найдем теперь площадь боковой поверхности пирамиды

$tt S_{bok}=dfrac{1}{2}cdot P_{OCH}cdot SK=dfrac{1}{2}cdot 4cdotdfrac{d}{2cosfrac{alpha}{2}}cdotdfrac{dsinalpha}{4cosfrac{alpha}{2}cosbeta}=dfrac{2d^2tgfrac{alpha}{2}}{cosbeta}$