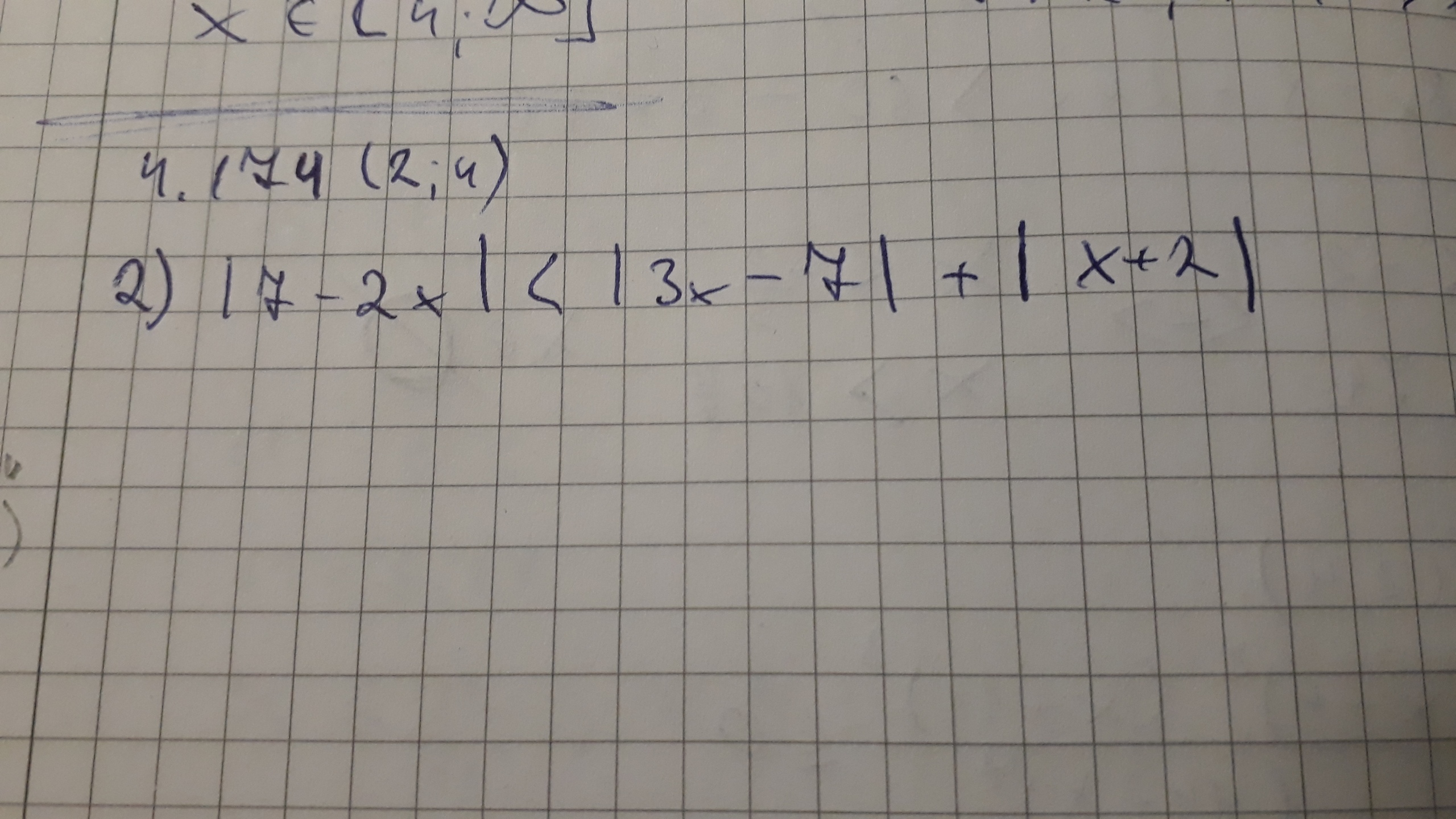помогите пожалуйста решить модульное неравенство методом интервалов

7-2*х>0⇒x<3,5; 3*x-7>0⇒x>2 1/3; х+2>0⇒x>-2

В диапазоне  от -2 до 2 1/3 имеем 7-2*х>7-3*x+x+2=9-2*x - верно во всём диапазоне.

При х<-2 имеем 7-2*х<7-3*х-x-2=5-4*x - верно во всём диапазоне

При х>3,5 имеем 2*х-7<3*x-7+x+2=4*х-5 - верно во всём диапазоне.

При 3,5>х>2 1/3 имеем 7-2*х<3*x-7+x+2=4*x-5 - верно во всё диапазоне

Ответ: верно во всём диапазоне значений х.