Предмет: Геометрия
Автор: aosgard1
Вопрос задан 7 лет назад

Площадь прямоугольного треугольника с острым углом 60◦
равна 2√3 см2. Найдите гипотенузу треугольника.

Приложения:

Ответы

Ответ дал: NNNLLL54

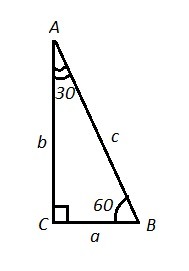
ΔАВС , ∠С=90° , ∠В=60° .

Обозначим ВС=а , АС=b , AB=c .

$S(Delta ABC)=frac{1}{2}cdot ab=2sqrt3; ; to ; ; ab=4sqrt3\\tg60^circ =frac{b}{a}; ; to ; ; sqrt3=frac{b}{a}; ; to ; ; b=asqrt3\\ab=acdot asqrt3=4sqrt3\\a^2cdot sqrt3=4sqrt3; ; to ; ; a^2=4; ,; ; a=2\\b=asqrt3=2sqrt3\\c^2=a^2+b^2=4+4cdot 3=16; ; to ; ; c=4\\underline {AB=4}$

P.S. Можно воспользоваться тем, что катет а лежит против угла в 30°, тогда он равен половине гипотенузы ⇒ гипотенуза в 2 раза длиннее этого катета , то есть с=2а=2·2=4

Приложения:

Ответ дал: армения20171

∆АВС ;<АСВ=90°;<ВАС=60°;S=2√3см²

AB=?
<ABC=90°-<BAC=90°-60°=30°
<30° против сторона равно половину гипотенуза
AC=AB/2

S=1/2*AB*AC*sin60°=2√3
1/2*AB*AB/2*√3/2=2√3
AB²=16
AB=4
гипотенуза триугольника 4см

Приложения:

Ответ дал: Аноним

помогите с заданем

Похожие вопросы

Окружающий мир

2 года назад

когда была 2мировая война

Қазақ тiлi

2 года назад

3 сөйлем құрау керек мынандай сөздерге екінші 40-50 жетеу деген сөздерге

Физика

2 года назад