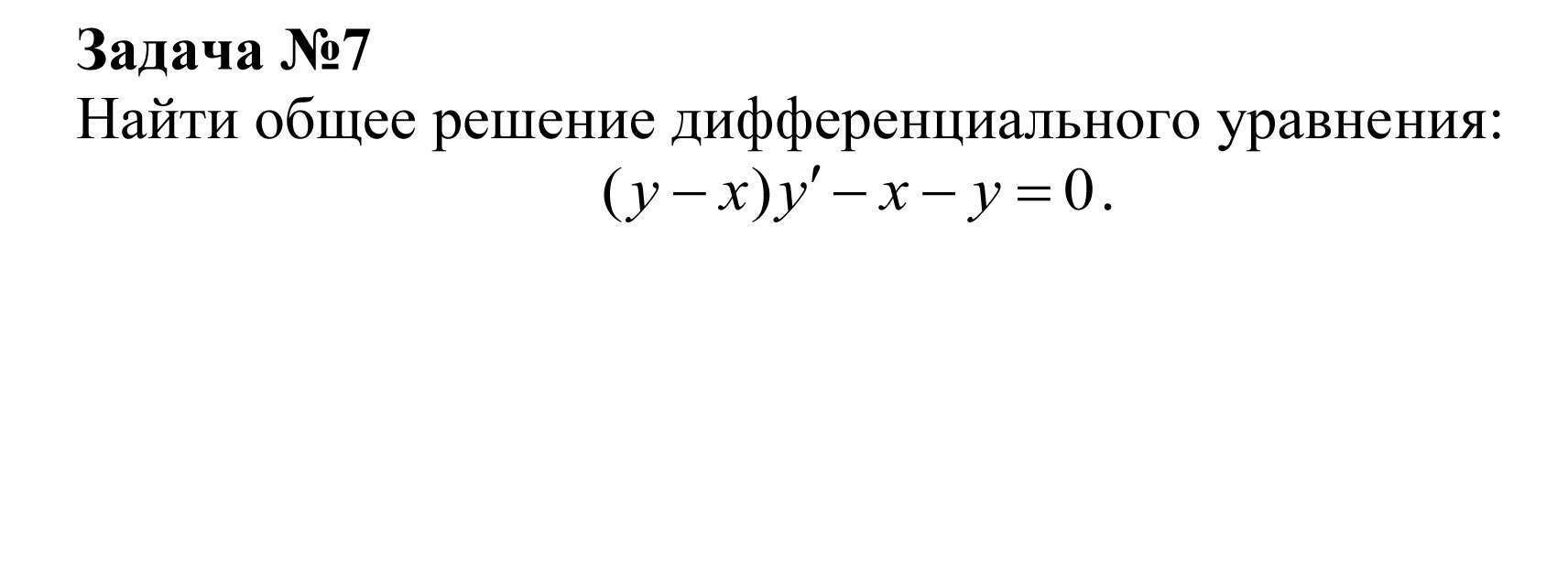Найти общее решение дифференциального уравнения:(с решением)

Приложения:

Ответы

Ответ дал: Аноним

Это дифференциальное уравнение первого порядка, разрешенное относительно производной, является однородным уравнением.

Пусть $tt y=ux$ , тогда $tt y'=u'x+u$

$tt (ux-x)(u'x+u)-x-ux=0\ (u-1)(u'x+u)=u+1\ \ u'x+u=dfrac{u+1}{u-1}\ \ u'x=dfrac{2}{u-1}+1-u$

Получили дифференциальное уравнение первого порядка, уравнение с разделяющимися переменными

$displaystyle tt frac{du}{dx}cdot x=dfrac{2}{u-1}+1-u\ \ frac{du}{dx}cdot x=-dfrac{(u-1)^2-2}{u-1}\ \ \ int frac{(u-1)du}{(u-1)^2-2}=int -xdx\ \ 0.5ln|(u-1)^2-2|=-frac{x^2}{2}+C$

Возвращаемся к обратной замене

$tt 0.5lnbigg|bigg(dfrac{y}{x}-1bigg)^2-2bigg|=-dfrac{x^2}{2}+C$ - общий интеграл

Похожие вопросы

Русский язык

2 года назад

помогите составить предложения по схемам

Русский язык

2 года назад

3 предложения с фрозеологизмом 3 класс

Русский язык

2 года назад

Напишите рассказ о предмете ХИМИЯ, почему он для вас является самым сложным, и что вы предпринимаете, для исправления ситуации? ОЧЕНЬ СРОЧНО

Алгебра

2 года назад

помогите пожалуйста

Литература

8 лет назад

что можно предположить об этой книге по её обложке ?

География

8 лет назад

напишите пожалуйста графическая схема полупустынь и пустынь. срочно.

Химия

9 лет назад

Уравнять методом электронного баланса, указать окислитель и восстановитель NaNO3 + Cu +H2SO4 = CuSO4 + NO + Na2SO4 + H2O

География

9 лет назад

1) первое место по добыче угля занимает бассейн а) печорский б) донецкий в) кузнецкий 2) экологически самый чистый вид топлива а) торф б) газ в) уголь