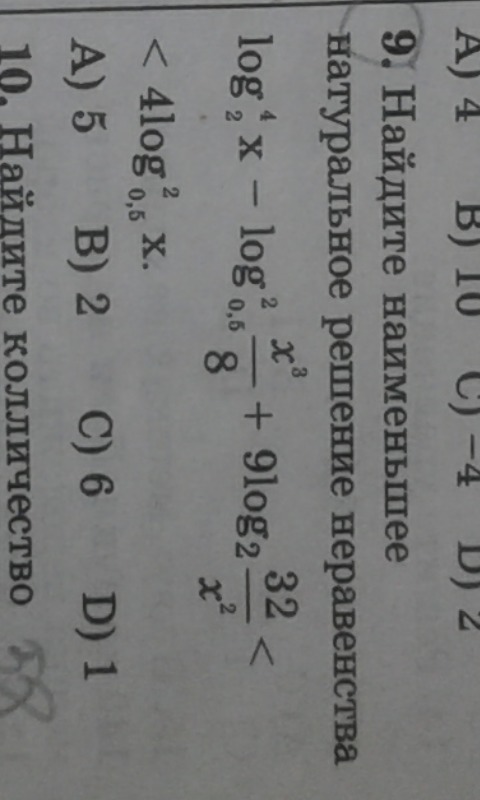Предмет: Математика
Автор: bestmusic
Вопрос задан 7 лет назад

Помогите пожалуйста решить неравенство (решение обязательно)

Приложения:

Ответы

Ответ дал: Единорожек34

$log_{2}^{4}x-log_{0,5}^{2}frac{x^3}{8}+9log_2 frac{32}{x^2}<4log_{0,5}^{2}x$
ОДЗ: x > 0
$log_{2}^{4}x-log_{2}^{2}frac{x^3}{8}+9log_2 frac{32}{x^2}<4log_{2}^{2}x\log_{2}^{4}x-(log_2x^3-log_28)^2+9log_232-9log_2x^2<4log_{2}^{2}x\log_{2}^{4}-(3log_2x-3)^2+45-18log_2x<4log_{2}^{2}x\log_{2}^{4}x-9log_{2}^{2}x+18log_2x-9+45-18log_2x<4log_{2}^{2}x\log_{2}^{4}-13log_{2}^{2}x+36<0\log_{2}^{2}x=t\t^2-13t+36<0\D=13^2-4*36=(13-2*6)(13+2*6)=25\t_1=frac{13+5}{2}=9\t_2=frac{13-5}{2}=4\(t-9)(t-4)<0\(log_{2}^{2}x-9)(log_{2}^{2}x-4)<0\(log_2x-3)(log_2x+3)(log_2x-2)(log_2x+2)<0\x_1=8; x_2=frac{1}{8}; x_3=4; x_4=frac{1}{4}$
_+_(1/8)_-_(1/4)_+__(4)_-_(8)_+_
$x in (frac{1}{8};frac{1}{4})cup(4;8)$
Наим. натуральное решение 5
Ответ: 5

Похожие вопросы

Английский язык

2 года назад

надо составить 6 предложений про семью

Русский язык

2 года назад

От глагола сгорбить можно образовать краткое причастие?

История

2 года назад

Помогите срочно пжжжжжжжжжжж

Русский язык

2 года назад