Решите пожалуйста, спасибо заранее

cosC = (CB*CA)/(|CB|*|CA|)

CB = (2 - 4; 14 - 0) = (-2; 14)
|CB| = sqrt(4 + 196) = sqrt(200) = 10*sqrt(2)

CA = (-4 - 4; 8 - 0) = (-8; 8)
|CA| = sqrt(64 + 64) = sqrt(128) = 8*sqrt(2)

CB*CA = -2*(-8) + 14*8 = 128

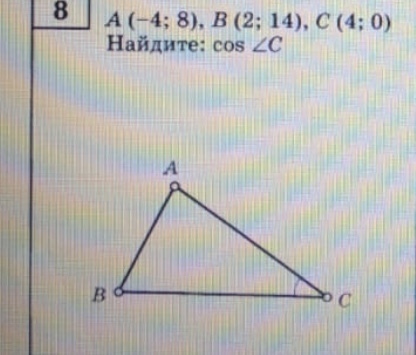
Найдём cos∠C, используя вектора СА(-8; 8) и СВ(-2; 14).

cos∠C = (СА · СВ)/(|CA|·|CB|) = (-8·(-2) + 8·14)/(√(64+64)·√(4+196)) =

= (8·16)/(8√2 · 10√2) = 16/20 = 4/5 = 0,8