Две параллельные прямые пересечена секущей разность двух из восьми образовавшейся угла равны 44 градусов найдите каждый из восьми углов
СРОЧНО!!!!!!!!

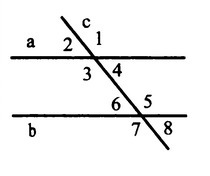
При пересечении двух параллельных прямых третьей (не под прямым углом) образуются 8 углов, четыре из которых имеют одну величину и четыре - другую:

На рисунке видны такие углы 1 и 3; 2 и 4, а так же 5 и 7; 6 и 8. Очевидно, что все эти пары представляют собой равные углы, так как являются вертикальными. Таким образом, мы имеем четыре бо'льших угла: 1, 3, 5, 7 и четыре меньших: 2, 4, 6, 8. Разность между бо'льшим и меньшим углом, по условию, равна 44°. Сумма большего и меньшего равна 180°. Тогда:

{ ∠1 - ∠2 = 44°

{ ∠1 + ∠2 = 180°    -  Складываем оба уравнения:

2 *∠1 = 224°   =>   ∠1 = 112°;    ∠2 = 180 - 112 = 68°

Таким образом: ∠1 = ∠3 = ∠5 = ∠7 = 112°

                            ∠2 = ∠4 = ∠6 = ∠8 = 68°