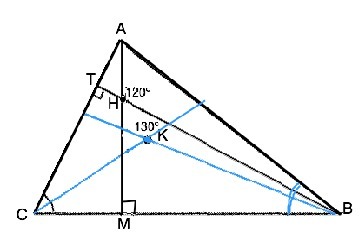
Высоты остроугольного треугольника ABC, проведенные из вершин A и B, пересекаются в точке H, причем угол AHB=120 , а биссектрисы, проведенные из вершин B и C — в точке K, причем угол BKC=130. Найдите угол ABC.
Ответы
Ответ дал:
0
Угол АНВ=120°, ⇒ смежный ему ∠АНТ=60°, ⇒ в прямоугольном треугольнике АНТ ∠НАТ=30°. В прямоугольном треугольнике САМ угол С=60°, и биссектриса делит его на два по 30°. В Δ СКВ ∠СКВ=130° ( дано). ⇒ ∠КВС=180°-∠ СКВ-∠КСВ=180°-130°-30°=20°. Так как ВК - биссектриса, угол АВС=2•20°=40°.
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад