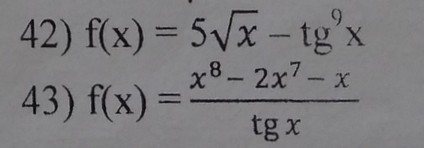Предмет: Алгебра
Автор: aygels
Вопрос задан 7 лет назад

< >

ПОМОГИТЕ, ПОЖАЛУЙСТА
НУЖНО НАЙТИ ПРОИЗВОДНУЮ

Приложения:

Ответы

Ответ дал: d3782741

0

Вспомним правила дифференцирования частного двух функций и производную тангенса

$f(x)=dfrac{g(x)}{h(x)} Rightarrow f'(x)=dfrac{g'(x)h(x)-g(x)h'(x)}{h^2(x)}$

Тогда:

$tan(x)=dfrac{sin(x)}{cos(x)} medskip \ left[tan(x)right]'=left[dfrac{sin(x)}{cos(x)}right]'=dfrac{(sin(x))'cos(x)-sin(x)(cos(x))'}{cos^2(x)}=medskip\=dfrac{cos^2(x)+sin^2(x)}{cos^2(x)}=dfrac{1}{cos^2(x)}$

Перейдем к примерам

$42)~f(x)=5sqrt{x}-tan^9(x) Leftrightarrow f(x)=5x^{frac{1}{2}}-tan^9(x) medskip \ f'(x)=dfrac{5}{2}x^{-frac{1}{2}}-9tan^8(x)cdotdfrac{1}{cos^2(x)}cdot 1=dfrac{5}{2sqrt{x}}-dfrac{9tan^8(x)}{cos^2(x)} medskip \ 43)~f(x)=dfrac{x^8-2x^7-x}{tan(x)} medskip \ f'(x)=dfrac{left(x^8-2x^7-xright)'cdottan(x)-left(tan(x)right)'cdotleft(x^8-2x^7-xright)}{tan^2(x)}=medskip\=dfrac{tan(x)left(8x^7-14x^6-1right)-frac{x^8-2x^7-x}{cos^2(x)}}{tan^2(x)}$

Приведем последний пример к более благородному виду

$dfrac{tan(x)left(8x^7-14x^6-1right)-frac{x^8-2x^7-x}{cos^2(x)}}{tan^2(x)}=dfrac{frac{sin(x)cos(x)left(8x^7-14x^6-1right)-x^8+2x^7+x}{cos^2(x)}}{tan^2(x)}=medskip\=dfrac{sin(x)cos(x)left(8x^7-14x^6-1)-x^8+2x^7+x}{sin^2(x)}=medskip\=dfrac{sin(2x)left(8x^7-14x^6-1right)-2x^8+4x^7+2x}{2sin^2(x)}$

Ответ.

$42)~f'(x)=dfrac{5}{2sqrt{x}}-dfrac{9tan^8(x)}{cos^2(x)}$ ;

$43)~f'(x)=dfrac{sin(2x)left(8x^7-14x^6-1right)-2x^8+4x^7+2x}{2sin^2(x)}$

Ответ дал: d3782741

0

Соответственно, tan(x)=tg(x). Просто другое его обозначение.

Похожие вопросы

Русский язык

2 года назад

Подбери к исенам прилагательным существительные.укажы в словах примое иле переносное значение.Горячая .Косолапый.золотое.весёлая.колючий.широкое.горячая.ловкий.банное.дружный.летний.весенние.

Українська мова

2 года назад

як пишеться слово мавп?ячий з апострофом чи без?

Математика

2 года назад

работа 1 класса пожалуйста помогите

Математика

2 года назад

Укажи число, в котором 15 единиц класса тысяч. а) 15 000 б) 15 в) 1 500 г) 150 000

Биология

8 лет назад

Пред история: Я очень люблю анатомию, могу заниматься ею вечно, но не могу выбрать подходящую профессию Мой вопрос таков: Подскажите пожалуйста, какие профессии связанны с этой наукой (кроме разных

История

8 лет назад

русско турецкая война 1768 1774 значение

История

9 лет назад

Какой компанией был изобретен цветной телевизор?

Геометрия

9 лет назад

луч OC делит угол AOB на два угла. найдите угол AOC если АОВ =108 градусов а угол АОС на 18 градусов меньше угла ВОС