СРОЧНО, ДАМ 30 БАЛЛОВ Внутри большего квадрата расположен меньший квадрат площади 61. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?
Приложения:
Ответы
Ответ дал:
0
сторона меньшего квадрата =✓61
(т.к. площадь квадрата =61)
является гипотенузой прямоугольного треугольника
,сумма катетов которого является длиной стороны большого квадрата.
то есть , с учётом теоремы Пифагора, нам осталось решить уравнение в целых, положительных числах
х²+у²=61 и найти Sбольшого квадрата= (х+у)²
простым перебором выясняем,
что х=5 у=6 (или наоборот) нам подходят, действительно,
5²+6²=25+36=61
Поэтому
х+у=11
а площадь Sбольшого квадрата= (х+у)²=
=11²=121
(т.к. площадь квадрата =61)
является гипотенузой прямоугольного треугольника
,сумма катетов которого является длиной стороны большого квадрата.
то есть , с учётом теоремы Пифагора, нам осталось решить уравнение в целых, положительных числах
х²+у²=61 и найти Sбольшого квадрата= (х+у)²
простым перебором выясняем,
что х=5 у=6 (или наоборот) нам подходят, действительно,
5²+6²=25+36=61
Поэтому
х+у=11
а площадь Sбольшого квадрата= (х+у)²=
=11²=121
Приложения:
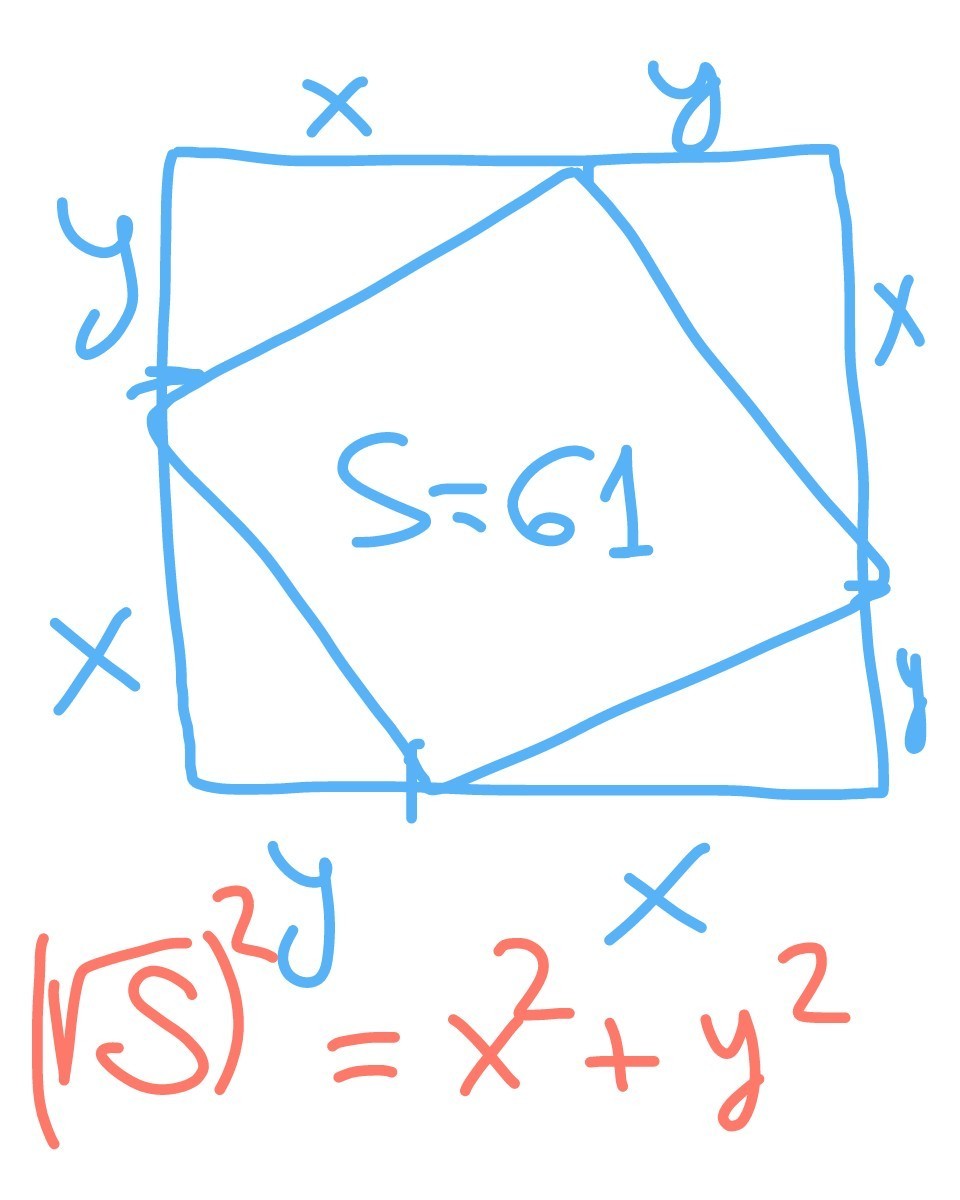
Ответ дал:
0
на здоровье! любопытная задачка;)
Ответ дал:
0
у меня есть ещё одна неплохая задачка :D
Ответ дал:
0
не получается решить, если площадь равна 53 . помогите пожалуйста
Ответ дал:
0
х²+у²=53 => х+у=49+4=7²+2²
Ответ дал:
0
спасибо ,уже решила :)
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад