Предмет: Алгебра
Автор: Abduramank
Вопрос задан 7 лет назад

Как решить такое уравнение?Если можно,расскажите по подробнее как вы это решаете.Уравнение из института

Приложения:

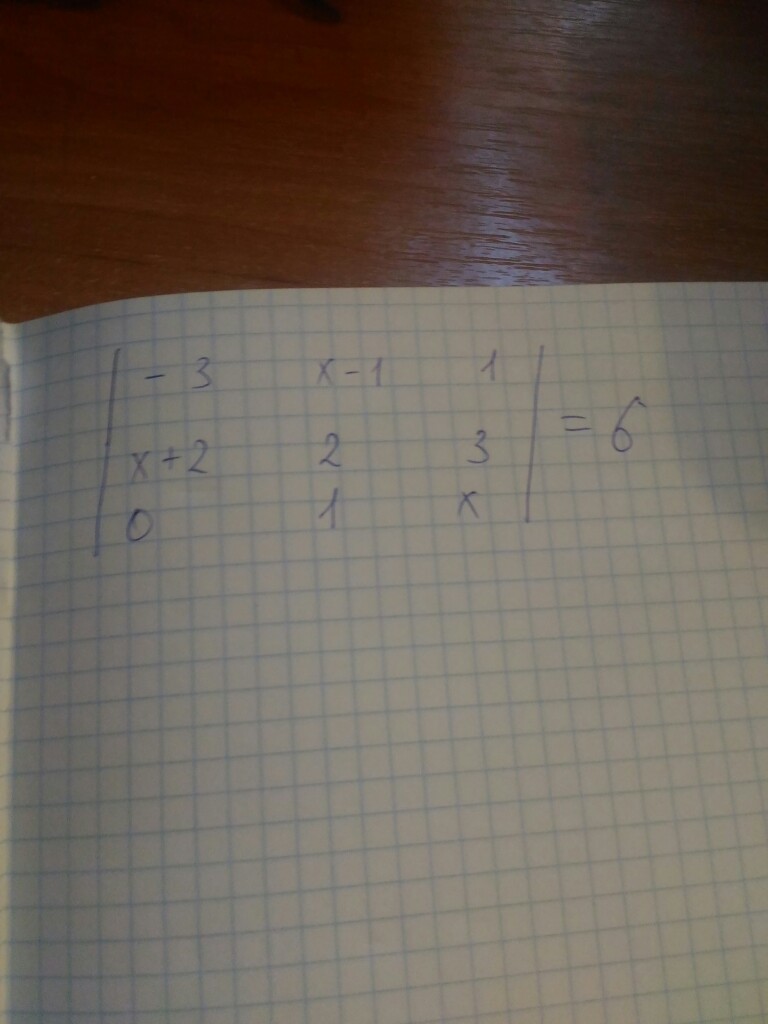
Ответы

Ответ дал: Аноним

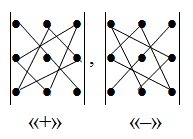
Решение определителя по правилу треугольников.(во вложении)

$left|begin{array}{ccc}-3&x-1&1\ x+2&2&3\ 0&1&xend{array}right|=(-3)cdot 2cdot x+(x-1)cdot 3cdot 0+(x+2)cdot 1cdot 1-\ \ -(1cdot2cdot0+(x+2)cdot(x-1)cdot x+1cdot 3cdot(-3))=-6x+x+2-(x^3+\ \ +x^2-2x-9)=-5x+2-x^3-x^2+2x+9=-x^3-x^2-3x+11=6\ \ -x^3-x^2-3x+5=0\ x^3+x^2+3x-5=0\ \ x^3+2x^2+5x-x^2-2x-5=0\ \ x^2(x-1)+2x(x-1)+5(x-1)=0\ \ (x-1)(x^2+2x+5)=0$

Произведение равно нулю, если хотя бы один из множителей равен нулю

$x-1=0~~~Rightarrow~~~ boxed{x=1}$

Уравнение $x^2+2x+5=0$ действительных корня не имеет, т.к. его дискриминант меньше нуля.

Ответ: 1.

Приложения:

Ответ дал: NNNLLL54

$left|begin{array}{ccc}-3&x-1&1\x+2&2&3\0&1&xend{array}right|=6$

Раскроем определитель по 1 столбцу:

$-3cdot (2x-3)-(x+2)cdot (x(x-1)-1)=6\\-6x+9-(x+2)(x^2-x-1)=6\\-6x+9-(x^3-x^2-x+2x^2-2x-2)=6\\x^3+x^2+3x-5=0\\x=1:; ; 1^3+1^2+3cdot 1-5=0; ; Rightarrow \\x^3+x^2+3x-5=(x-1)(x^2+2x+5)=0\\x^2+2x+5=0; ,; ; D=4-20=-16<0; ; Rightarrow ; ; x^2+2x+5>0; pri; xin R\\otvet:; ; x=1.$