Предмет: Математика
Автор: petuhovsas2017
Вопрос задан 7 лет назад

< >

Помогите пожалуйста!
Решить систему методом Крамера и матричным методом
Хотя бы 1 уравнение

Приложения:

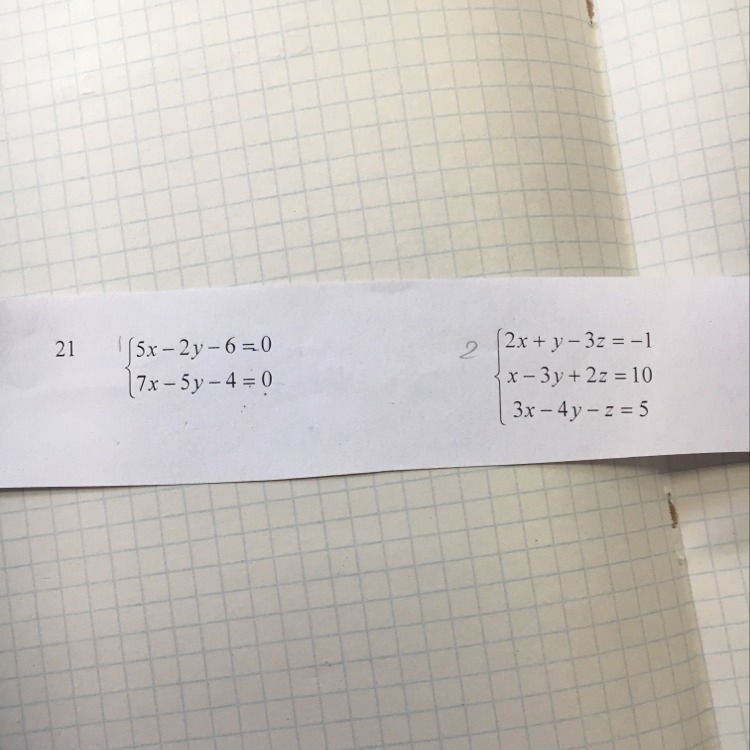
Ответы

Ответ дал: NNNLLL54

0

$1); ; left{begin{array}{cc}5x-2y=6\7x-5y=4end{array}right; ; ; Delta =left|begin{array}{cc}5&-2\7&-5end{array}right|=-25+14=-11ne 0\\\Delta _{x}=left|begin{array}{cc}6&4\-2&-5end{array}right|=-30+8=-22\\\Delta _{y}=left|begin{array}{cc}5&7\6&4end{array}right|=20-42=-22\\\x=frac{Delta _{x}}{Delta }=frac{-22}{-11}=2; ; ,; ; y=frac{Delta _{y}}{Delta }=frac{-22}{-11}=2$

$2); ; left{begin{array}{ccc}2x+y-3z=-1\x-3y+2z=10\3x-4y-z=5end{array}right; ; ,; ; A=left(begin{array}{ccc}2&1&-3\1&-3&2\3&-4&-1end{array}right)\\\detA=2(3+8)-(-1-6)-3(-4+9)=14\\A_{11}=11; ; ,; ; A_{12}=-(-7)=7; ; ,; ; A_{13}=5\\A_{21}=-(-13)=13; ; ,; ; A_{22}=7; ; ,; ; A_{23}=-(-11)=11\\A_{31}=-7; ; ,; ; A_{32}=-7; ; ,; ; A_{33}=-7\\\A^{-1}=frac{1}{14}cdot left(begin{array}{ccc}11&13&-7\7&7&-7\5&11&-7end{array}right)\\\X=A^{-1}cdot B=frac{1}{14}cdot left(begin{array}{ccc}11&13&-7\7&7&-7\5&11&-7end{array}right)cdot left(begin{array}{ccc}-1\10\5end{array}right)=$

$=frac{1}{14}cdot left(begin{array}{ccc}84\28\70end{array}right)=left(begin{array}{ccc}6\2\5end{array}right)$

Ответ дал: petuhovsas2017

0

А как это понимать?

Ответ дал: NNNLLL54

0

перезагрузи страницу, не с телефона, редактор формул отобразит формулы

Похожие вопросы

Английский язык

2 года назад

Complete the sentences with the correct question tags. 1) You can give the first aid to someonewho is injured,____________________ 2) His friend was sent to the hospital

Русский язык

2 года назад

Спишите текст, вставляя пропущенные буквы и выбирая из скобок нужное причастие. В причастиях выделите суффиксы и определите вид причастия. Подчеркните причастные обороты как член предложения и там,

Литература

2 года назад

Какова причина «бестолковых поминок»? ( Достоевский )

Физкультура и спорт

2 года назад

1. Назовите особенности техники торможения плугом 2. Перечислим зимние виды спорта

Математика

8 лет назад

решите пожалуйста просто срочно надо

Математика

8 лет назад

срочно помогите с алгеброй

Математика

9 лет назад

рабочий 8 часовой рабочий день Вытачевает 80 деталей а его ученик работает 6 часов в день и вытачивает 42 таких деталей На сколько больше деталей выточил за 1 час рабочий чем его ученик Измени вопрос

Математика

9 лет назад

ско лько будет г в 2ц 30кг