Найдите все числа, которые при делении на 3 дают остаток 1, а при делении на 5 дают остаток 3.
Ответ запишите в виде формулы, используя неизвестную "n".
Например, все чётные числа: "2n".Например, числа, которые при делении на 5 дают остаток 3: "5n+3". И объясните.
Ответы
Ответ дал:
0
.........................................................................................
Приложения:
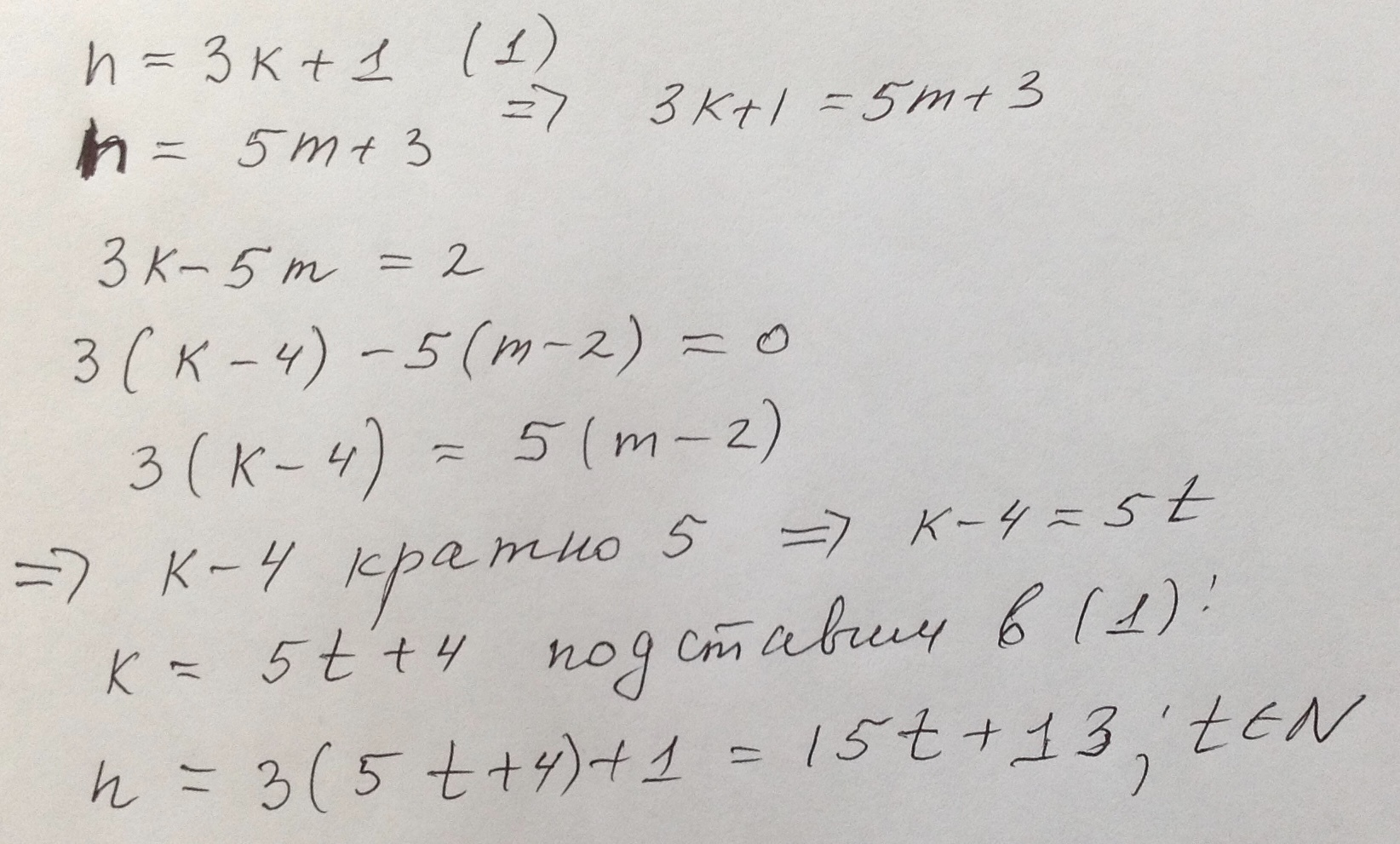
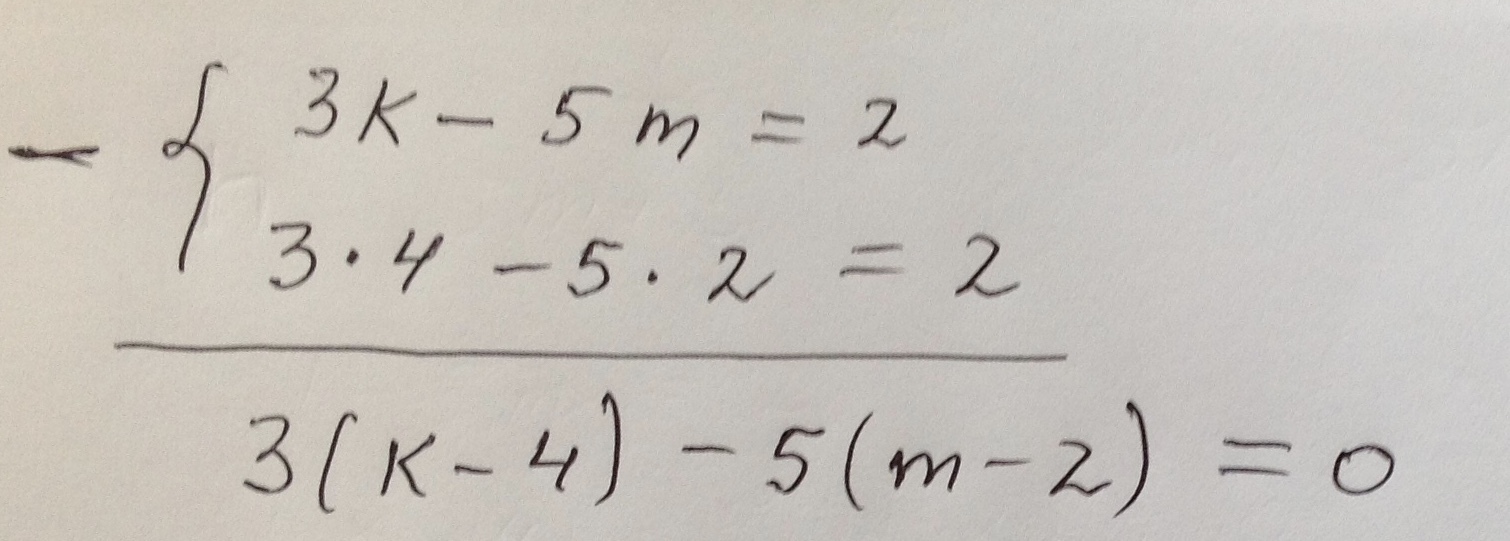
Ответ дал:
0
n=5m+3 (опечатка во 2 строчке)
Ответ дал:
0
ага, а то что то я запутался)
Ответ дал:
0
Вообщем спасибо. Хоть мне больше понятен был ответ Зинаиды, но за старанее спасибо)
Ответ дал:
0
старание*
Ответ дал:
0
происхождение 4 строчки ( добавил лист)
Ответ дал:
0
1) Составим ряд чисел, которые при делении на 5 дают остаток 3:
8; 13; 18; 23; 28; 33; 38; 43; 48; 53; 58; ....; 5n+3;....
2) Выберем из них те числа, которые при делении на 3 дают остаток 1:
13; 28; 43; 58; ...; 15n-2;...
Ответ: 15n-2;
Приложения:
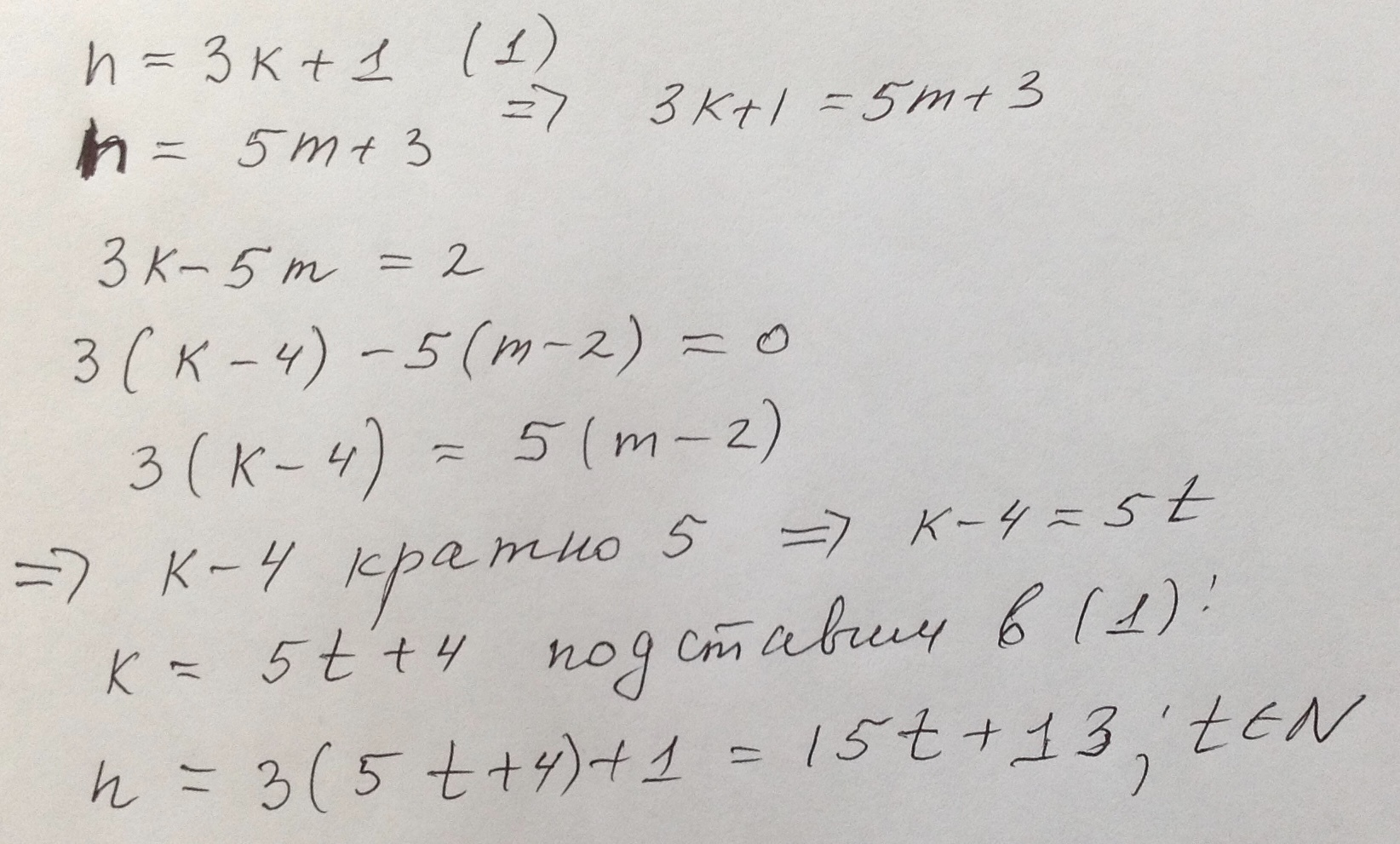
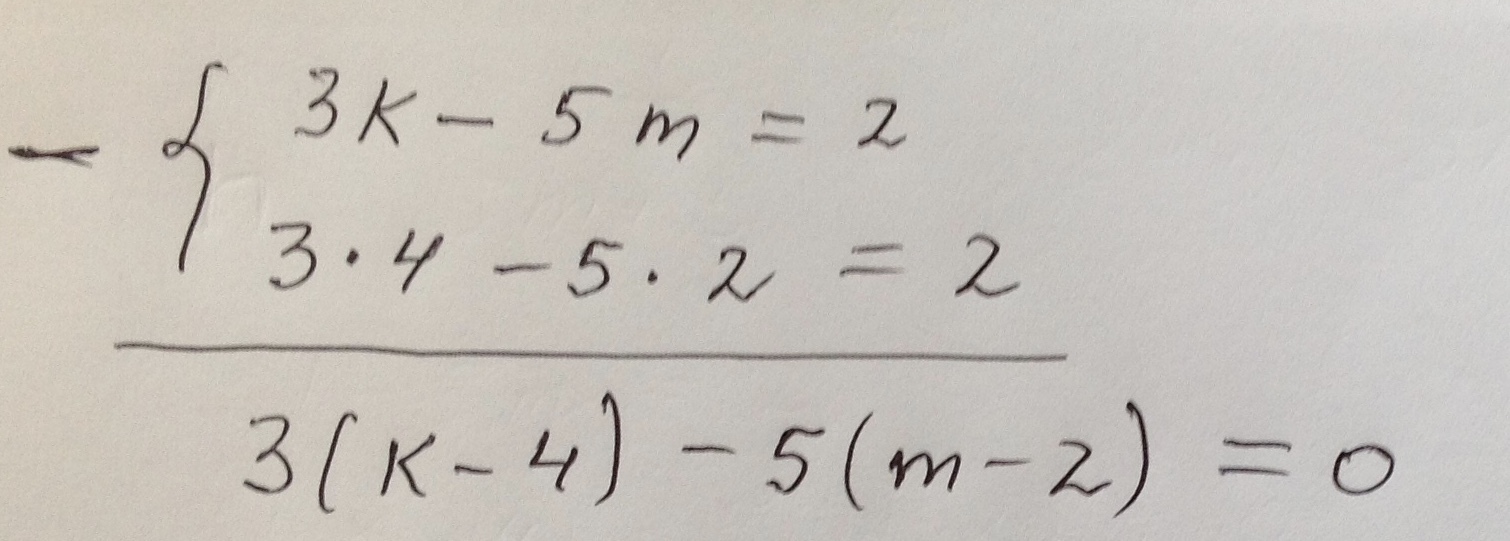
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад