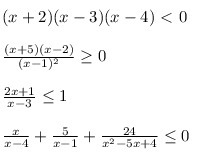Помогите, пожалуйста, решить неравенства:

$(x+2)(x-3)(x-4) textless 0\\frac{(x+5)(x-2)}{(x-1)^2} geq 0\\frac{2x+1}{x-3} leq 1\\frac{x}{x-4} + frac{5}{x-1} + frac{24}{x^2 -5x +4} leq 0$

Приложения:

Ответы

Ответ дал: mmb1

везде применяем метод интервалов

(x+2)(x-3)(x-4) < 0

------------ (-2) +++++++++ (3) ------------- (4) ++++++++++

x∈(-∞ -2) U (3 4)

(x+5)/(x-2)/(x-1)^2 >=0

++++++++++ [-5] ------------ (1) ------------ [2] +++++++++++

x∈(-∞ -5] U [2 +∞)

(2x+1)/(x-3) <=1

(2x+1)/(x-3) - 1<=0

(2x+1 - x + 3)/(x-3)<=0

(x+4)/(x-3)<=0

+++++++ [-4] ------------- (3) +++++++

x∈[-4 3)

x/(x-4) + 5/(x-1) + 24/(x-1)(x-4) <=0

(x(x-1) + 5(x-4) + 24)/(x-1)(x-4) <=0

(x^2 - x + 5x - 20 + 24) /(x-1)(x-4) <=0

(x^2-4x+4)/(x-1)(x-4) <=0

(x-2)^2/(x-1)(x-4) <=0

++++++++ (1) -----------[2] ---------- (4) ++++++++

x∈(1 4)

Ответ дал: id184272144

Спасибо, огромное! Т.е. вы приравняли к нулю и потом на координатной прямой отметили эти полученные цифры и потом исходя из знака больше или равно написали ответ?

Ответ дал: mmb1

я вам написал - применяется метод интервалов
он состоит из 4-х частей
почитайте -
здесь нет места для объяснений

Похожие вопросы

Русский язык

2 года назад

Подчеркни слова, в которых можно проверить безударную гласную: На большой поляне, в сосновом лесу ребята устроили кормушку для птиц.

Английский язык

2 года назад

англ яз помогите прошу вас срочно 5 номер

Биология

2 года назад

изменяется ли дыхание при понижении или повышении артериального давления?