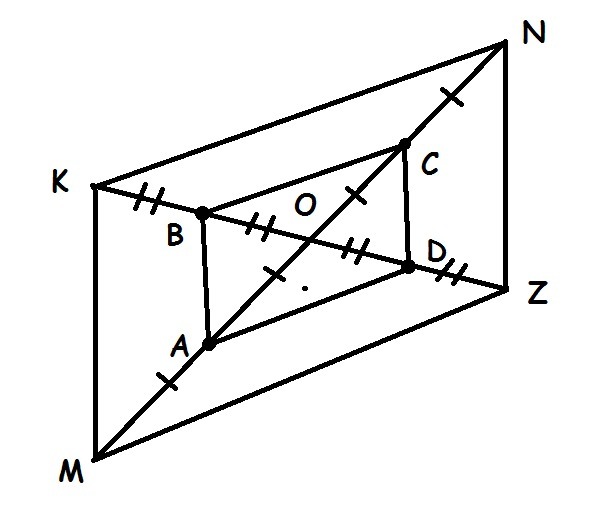
В параллелограмме MKNZ диагонали пересекаются точке O Докажите что что четырехугольник ABCD вершинами которого являются середины отрезков OM, OK, ON и OZ - параллелограм
Ответы
Ответ дал:
0
Рассмотрим параллелограмм MKNZ.
MO = ON, KO = OZ т.к. диагонали параллелограмма в точке пересечения делятся пополам
MA = AO, OC = CN по условию.
AO = MO : 2, OC = ON : 2 По условию.
MO = ON Из этого следует, что AO = OC
KB = BO, OD = DZ по условию.
BO = KO : 2, OC = OZ : 2 По условию.
KO = OZ Из этого следует, что BO = OD
Рассмотрим четырёхугольник ABCD
Диагональ BD в точке О делит диагональ AC на 2 равных отрезка
Диагональ AC в точке О делит диагональ BD на 2 равных отрезка
Ответ: Четырёхугольник ABCD является параллелограммом т.к. его диагонали делятся пополам в очке пересечения.
Приложения:
Ответ дал:
0
"в очке" ахахах
Ответ дал:
0
:D
Ответ дал:
0
))
Ответ дал:
0
спасибо большое
Ответ дал:
0
спасибо
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад