В треугольнике abc ab =ac.медиана к боковой стороне делит высоту проведённую к основанию на отрезке больший из которых равен 8,найти длинн этой высоты

abc - равнобедренный => высота, проведенная к основанию является также медианой.
Медианы точкой пересечения делятся на отрезки, которые относятся как 2:1 => 8:х=2:1; х=4
высота = 8+4=12
ответ: 12

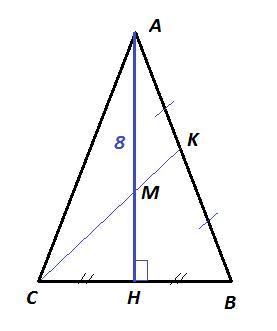
ΔABC : AB=AC;  AK=KB;  AH⊥CB; AM = 8

Высота в равнобедренном треугольнике, проведенная к основанию, также является медианой :

AB=AC;  AH⊥CB;  ⇒   CH=HB,  AH - медиана

В любом треугольнике медианы точкой пересечения делятся в отношении 2:1 , считая от вершины :

AH = AM + MH = 8 + 4 = 12

Ответ : 12