СРОООООЧНОО ДАМ 25 БАЛЛОВ ПОМОГИТЕ
площадь фигуры, ограниченная шортами?формула этого задания
Приложения:
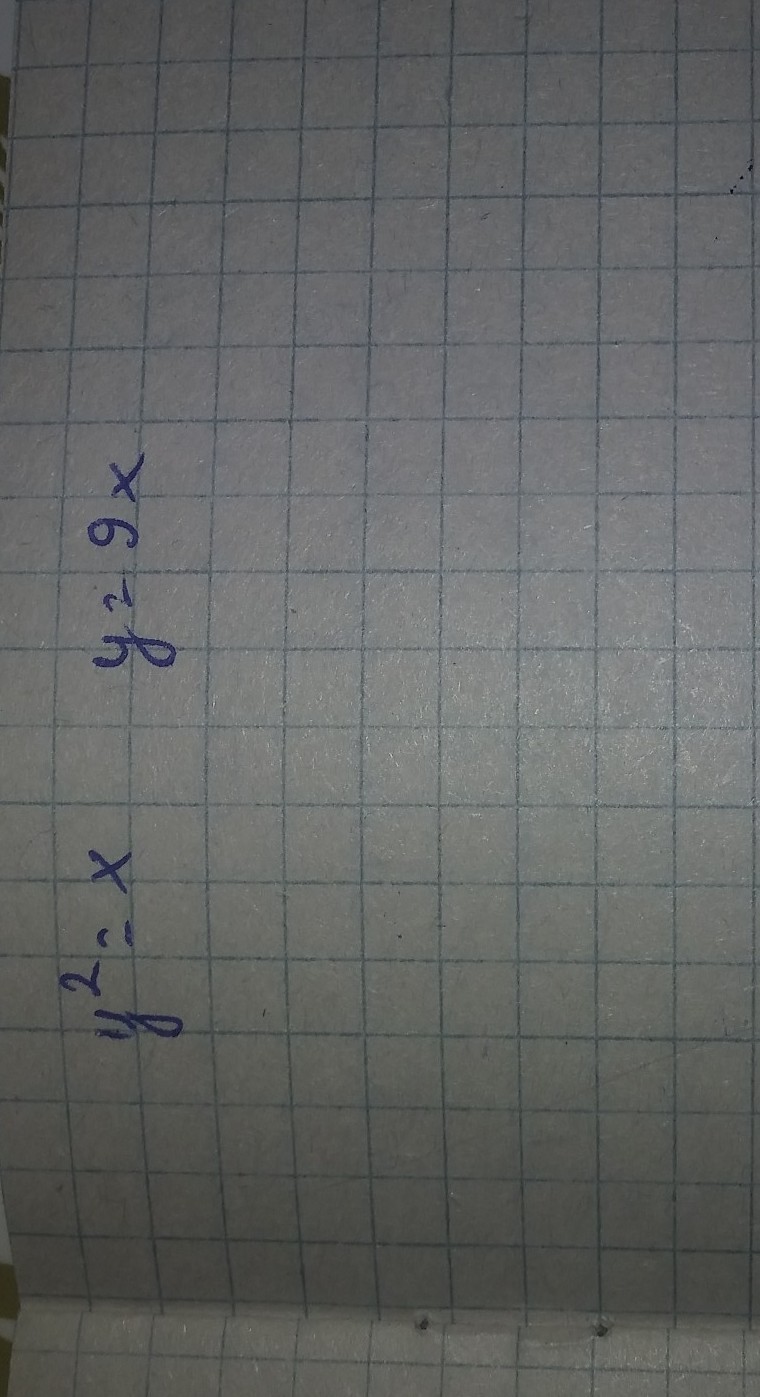
Ответы
Ответ дал:
0
ДАНО:
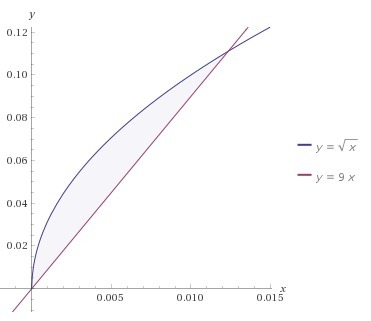
y(x) = √x = x¹/² и f(x) = 9*x
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
Находим пределы интегрирования решив равенство y(x) = f(x).
x¹/² = 9*x, x = 81*x²
a = 1/81 - верхний предел , b = 0 - нижний предел,
Находим разность функций - функция y(x) выше, чем функция f(x)
s(x) = x¹/² - 9*x - исходная функция площади - интегрируем.
Вычисляем, подставляя верхний предел - а. S(0)=0,
S(a) = 1/4374 - площадь - ОТВЕТ.
Рисунок к задаче в приложении.
Приложения:
Ответ дал:
0
спасиба
Ответ дал:
0
первообразная неверно записана: инт(х^{1/2})dx=2/3*x^{3/2}, а не 2/3*х^{-2/3}
Ответ дал:
0
Исправлено.
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад