Найти угол под которым видны боковые стороны трапеции из точки пересечения биссектрис её острых углов.
Ответы
Ответ дал:
0
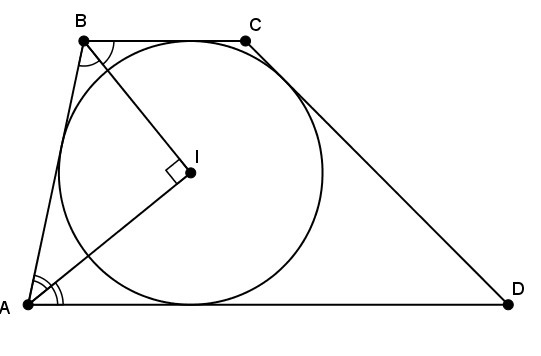
Сумма углов трапеции, прилежащих к боковым сторонам, равна 180°. Поэтому сумма углов ABI и IAB (см. рисунок; I — точка пересечения биссектрис) равна
Поскольку сумма треугольника равна 180°, то угол AIB равен 180°–90°=90°.
Для стороны CD проводятся аналогичные рассуждения.
Ответ: стороны видны под прямым углом.
***
Если мой ответ оказался полезен, смело отмечайте его как «лучший ответ».
Приложения:
Ответ дал:
0
спасибо большое , не мог бы ещё на вопрос ответить выставила только что
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад