Предмет: Математика
Автор: egri
Вопрос задан 7 лет назад

разложить многочлен (2(t^2)+3)/((t^3)+3t) ответ я знаю, но я не могу расписать как он получен, нужно как то методом неопределенных коофецентов я пологаю

Приложения:

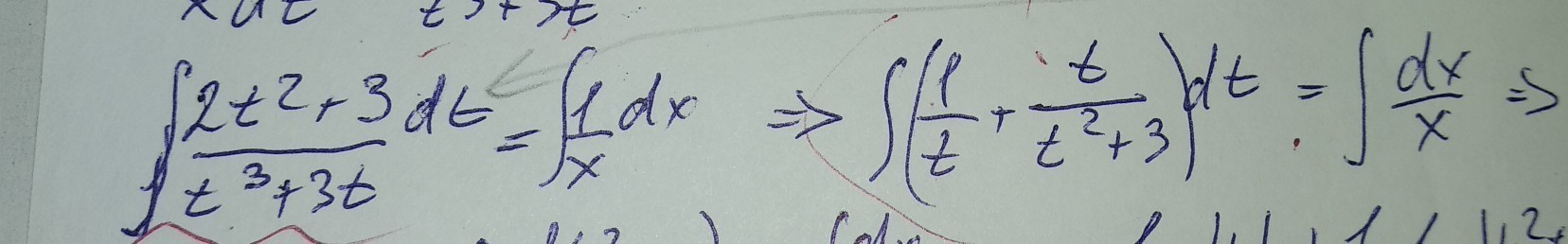
Ответы

Ответ дал: spasibo3pajbrh

$int frac{2 {t}^{2} + 3}{ {t}^{3} + 3t} dt = int frac{2 {t}^{2} + 3}{t ({t}^{2} + 3)} dt$
$frac{2 {t}^{2} + 3}{ t({t}^{2} + 3)} = frac{a}{t} + frac{bt + c}{ {t}^{2} + 3 } = \ = frac{a {t}^{2} + 3a + b {t}^{2} + ct}{t({t}^{2} + 3) } = \ = frac{(a + b) {t}^{2} + ct + 3a}{t({t}^{2} + 3)} \ (a + b) {t}^{2} + ct + 3a = \ = 2 {t}^{2} + 3 \$
приравнивается равные коэффициенты при одинаковых степенях t
$left { {{a + b = 2} { : : : : c= 0}atop {3a = 3}} right. = > \ left { {{a = 1} { : : : b= 1}atop {c = 0}} right.$
поэтому
$int frac{2 {t}^{2} + 3}{ t({t}^{2} + 3)} dt= \ = int frac{1}{t} dt + int frac{tdt }{ {t}^{2} + 3 } = \ = ln |t| + int frac{1}{2} frac{d( {t}^{2} + 3) }{ {t}^{2} + 3 } = \ = ln( |t| ) + frac{1}{2} ln( | {t}^{2} + 3| ) + c = \ = ln( |t| ) + frac{1}{2} ln( {t}^{2} + 3) + c$

Похожие вопросы

Русский язык

2 года назад

10 словосочетаний с предложным падежом 1, 2, 3 склонения

Русский язык

2 года назад

скажите, пожалуйста какой корень в слове "зрителей" СРОЧНО!

Информатика

2 года назад

пожалуйста помогите

Русский язык

2 года назад