из внутренней точки О треугольника ABC-проведены прямые,параллельные сторонам AB и BC.Эти прямые пересекают сторону AC в точках P и Q соответственно.Найдите прощадь треугольника POQ,если PQ=2,AC=1 и площадь треугольника ABC равна 98
Ответы
Ответ дал:
0
Пусть условие: "Из внутренней точки О треугольника ABC проведены прямые, параллельные сторонам AB и BC. Эти прямые пересекают сторону AC в точках P и Q соответственно. Найдите площадь треугольника POQ, если PQ=1, AC=2 и площадь треугольника ABC равна 98". Тогда решение:
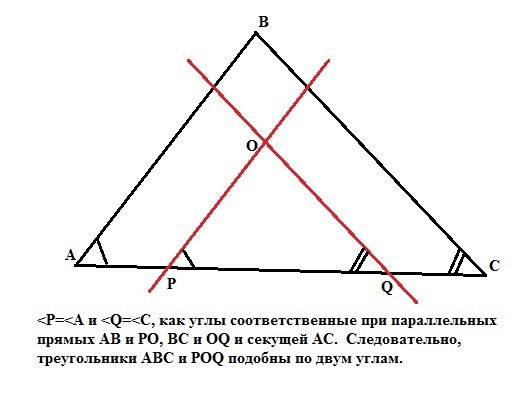
Соответственные стороны треугольников POQ и ABC параллельны, следовательно, углы треугольников, образованные этими сторонами, равны. Значит треугольники подобны с коэффициентом подобия k = PQ/AC = 1/2.
Площади подобных треугольников относятся как квадрат подобия, то есть Spoq/Sabc = 1/4 => Spoq = 98/4 = 24,5 ед².
Ответ: Spoq = 24,5 ед².
Если же PQ =2, а АС = 7, то k = 2/7 и соответственно
Spoq = 98*4/49 = 8 ед².
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад