Предмет: Алгебра
Автор: Mint777
Вопрос задан 7 лет назад

расположите в порядке возрастания числа tg 10; sin 10; cos 10; ctg 10

Ответы

Ответ дал: Artem112

Возьмем приближенно $pi approx3.14$

Рассмотрим число $10$ . На числовой окружности этому числу соответствует та же точка, что и числу $10-2pi$ :

$10-2piapprox10-2cdot3.14=3.72$

Зная, что $pi approx3.14$ и $dfrac{3pi}{2} approx4.71$ , получаем, что число $3.72$ располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.

Заметим, что число $3.72$ располагается ближе к числу $pi$ , так как $|3.72-pi|<left|dfrac{3pi}{2}-3.72right|$ .

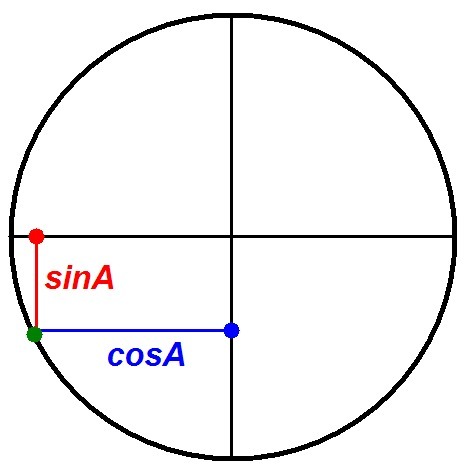
Зарисуем схематично число в 3 четверти, расположенное ближе к числу $pi$ . По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):

$cos10<sin10<0$

Рассмотрим тангенс. Так как тангенс положительный, то заменим отношение синуса к косинусу отношением их модулей:

$mathrm{tg}10=dfrac{sin10}{cos10} =dfrac{|sin10|}{|cos10|}$

Зная, что $cos10<sin10<0$ , получим, что $|cos10|>|sin10|$ , соответственно дробь $dfrac{|sin10|}{|cos10|}$ правильная, значит $mathrm{tg}10<1$ . Тогда, так как котангенс есть величина, обратная тангенсу, то $mathrm{ctg}10>1$ .