1. Из центра окружности , вписанной в треугольник со сторонами 10 см, 10 см и 12 см, к плоскости треугольника восстановлен перпендикуляр , длиной 4 см . Найдите расстояние от вершины перпендикуляра до сторон треугольника.
2. Точка М , лежащая вне плоскости равностороннего треугольника со стороной 3 см , находится на расстоянии √3 см от его плоскости . Найдите расстояние от точки М до сторон треугольника.
Ответы
Ответ дал:
0
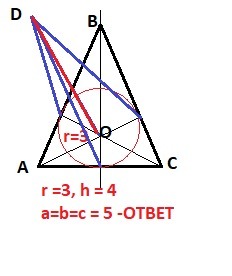
Задача 1.
Радиус вписанной окружности по формуле
Рисунок к задаче в приложении.
Получаем треугольники со сторонами 3:4:5 - "египетский"
ОТВЕТ 5 см одинаково для всех сторон.
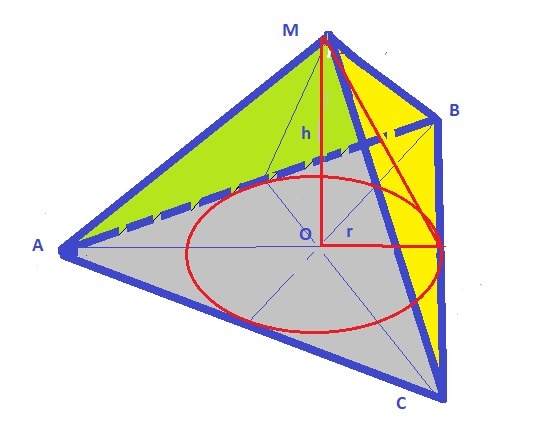
2. Рисунок к задаче в приложении. (Вариант годится и для первой задачи.)
1) Радиус вписанной окружности для правильного треугольника по формуле:
2) Расстояние до сторон по теореме Пифагора:
L² = (√3/2)² + (√3)² = 3 3/4 = 15/4
L = √(15/4) = 1/2*√3*√5 - расстояние до сторон - ОТВЕТ
Приложения:
Ответ дал:
0
L = √(15/4) = 1/2*√3*√5 - расстояние до сторон
Ответ дал:
0
Ответьте срочно
Ответ дал:
0
Это и есть ответ, но ... L = V(15)/2 - не красивый.
Ответ дал:
0
ааа ясно
Ответ дал:
0
добрый вечер!не могли бы вы помочь мне с задачами по геометрии на моей страничке?это ОЧЕНЬ срочно.заранее огромное спасибо
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад