ДАМ 50 БАЛЛОВ
Точка K удалена от каждой из вершин квадрата ABCD, сторона которого равна 6√2, на расстояние, равное 10.
Найдите расстояние от точки K до плоскости квадрата.

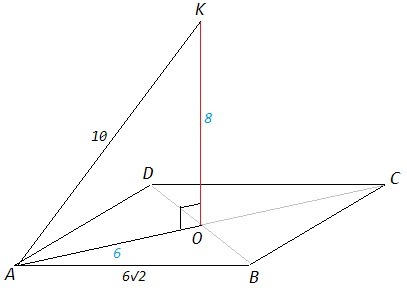
Точка K равноудалена от вершин квадрата, т.е. имеем правильную пирамиду KABCD, вершина K проецируется в точку пересечения диагоналей ABCD.

AO=AB√2/2 =6 (половина диагонали квадрата)

KO=8 (△KAO - египетский треугольник, множитель 2)

Точка K лежит на общем серединном перпендикуляре отрезков AC и BD, у отрезков общий центр O. Прямая, перпендикулярная двум прямым в плоскости, перпендикулярна самой плоскости, KO⊥(ABC).