Решите пж дам 30 баллов

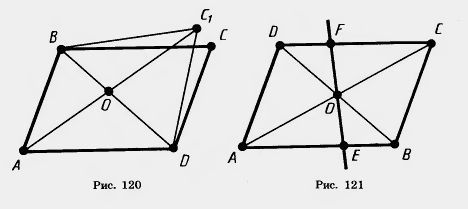
Доказательство. Пусть ABCD — данный параллелограмм (рис. 120). Проведем его диагональ BD. Отметим на  ней середину О и на продолжении отрезка АО отложим отрезок ОС1, равный АО.

По теореме 6.1 четырехугольник ABC1D есть параллелограмм. Следовательно, прямая ВС1 параллельна AD. Но через точку В можно провести только одну прямую, параллельную AD. Значит, прямая ВС1 совпадает с прямой ВС.

Точно так же доказывается, что прямая DC1 совпадает с прямой DC.

Значит, точка С1 совпадает с точкой С. Параллелограмм ABCD совпадает с ABC1D. Поэтому его диагонали пересекаются и точкой пересечения делятся пополам. Теорема доказана.

Свойство диагоналей параллелограмма