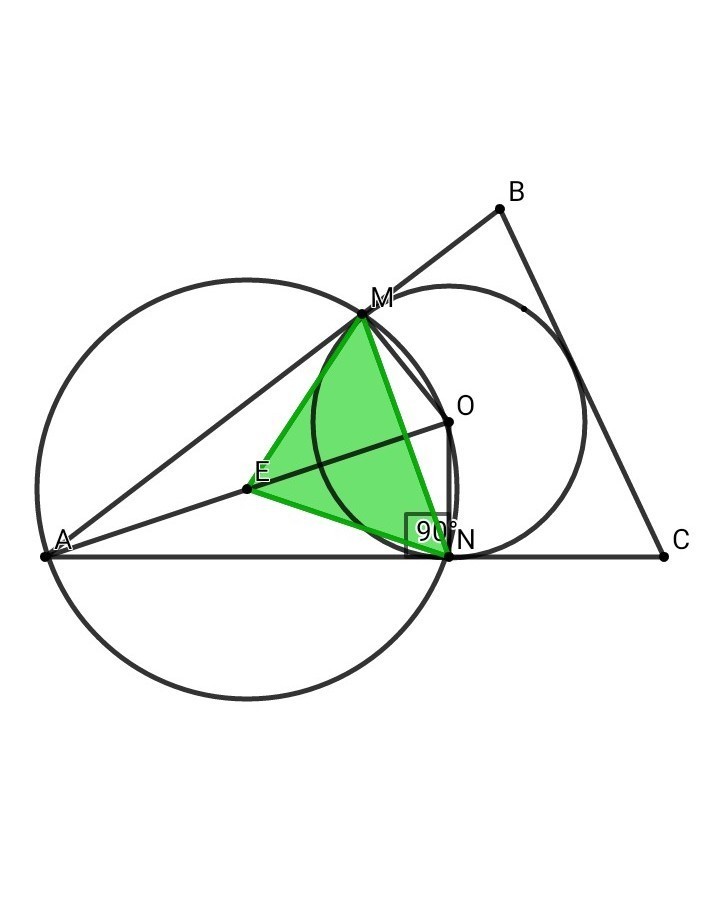
В треугольник ABC вписана окружность с центром O. Точки M и N - точки касания вписанной окружности со сторонами AB и AC соответственно. Найдите ∠A, если известно, что AO=2 MN.

• Отметим на отрезке АО середину в точке Е: АЕ = ЕО
АЕ = ЕО = MЕ = ЕN - по свойству прямоугольных треугольников АMО и АNO: медиана, проведённая из вершины прямого угла прямоугольного треугольника к гипотенузе, равна её половине.
ME = EN = MN => тр. EMN - равносторонний
угол MEN = 60°
• угол AMO + угол ANO = угол MAN + угол MON = 180°
Около четырёхугольника AMON можно описать окружность ( точка Е - центр окружности )
U MON = угол MEN = 60°
угол МАN = ( 1/2 ) • U MON = ( 1/2 ) • 60° = 30°

ОТВЕТ: 30°

Спасибо)