Один из углов, полученных при пересечении двух прямых, на 30° больше
другого. Найдите градусную меру бо́льшего угла, образованного этими
прямыми.
Ответы
Ответ дал:
0
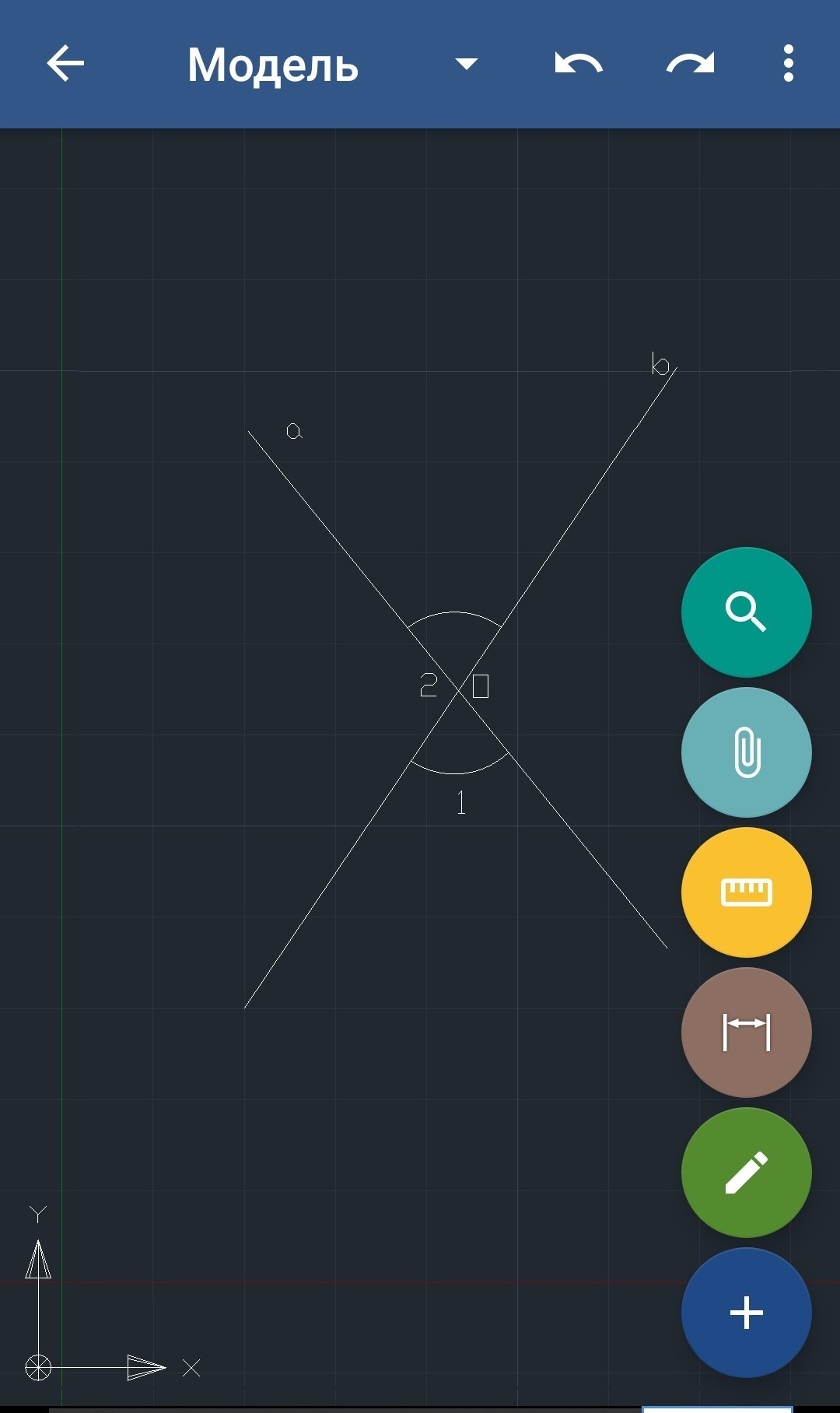
Дано:
а;b прямые
Угол 1 > угла 2 на 30°
Найти:
<1-?
Решение:
1)Сумма смежных углов равна 180°
Тогда составим уравнение.
Пусть большой угол - х°
Тогда меньший угол равен х°-30°
И их сумма равна 180°

105° боьтшый угол (Первый)
105°-30°=75° (Второй)
Ответ: 105° - боьтшый угол.
Примечание:
Не было рассмотрено вк других угла, так как при пересечении двух прямых образуется четыре угла, равных между собой, (Вертикальные углы равны)
а;b прямые
Угол 1 > угла 2 на 30°
Найти:
<1-?
Решение:
1)Сумма смежных углов равна 180°
Тогда составим уравнение.
Пусть большой угол - х°
Тогда меньший угол равен х°-30°
И их сумма равна 180°
105° боьтшый угол (Первый)
105°-30°=75° (Второй)
Ответ: 105° - боьтшый угол.
Примечание:
Не было рассмотрено вк других угла, так как при пересечении двух прямых образуется четыре угла, равных между собой, (Вертикальные углы равны)
Приложения:
Ответ дал:
0
2х=210, х=210:2=105
Ответ дал:
0
Тогда их сумма 315° что противоречит условию и свойству
Ответ дал:
0
херня
Ответ дал:
0
всё правильно 105-30=75 105 + 75=180
Ответ дал:
0
За исключением примечания. При пересечении двух прямых образуется четыре угла, ПОПАРНО равных.
Ответ дал:
0
Ответ:
решение представлено на фото
Объяснение:
Приложения:

Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад