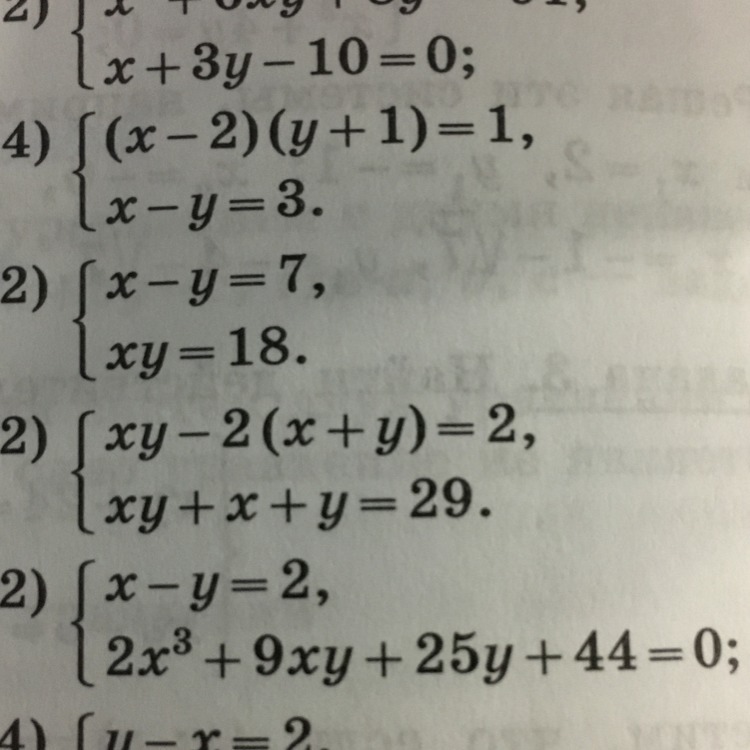Ответы
1) (1) xy-2(x+y)=2
(2) xy+x+y=29
вычтем из (1) - (2): -3x-3y=-27 (3)
вычтем из (2) - (1): 3x+3y=27 (4)
Мы пришли к равносильной системе.
Выходит, что x+y=9. Тогда xy=20(из 2 равенства)
Имеем систему: x+y=9 (*)
xy=20 (**)
Из (*)⇒ y=9-x. Тогда x(9-x)=20
x^2-9x+20=0. x=4(y=5) или x=5(y=4).
Ответ: (4;5),(5;4).
2) x-y=2 (1)
2x^3+9xy+25y+44=0 (2)
Из (1)⇒ y=x-2. Тогда 2x^3+9x(x-2)+25(x-2)+44=0
2x^3+9x^2+7x-6=0.
8x^3+36x^2+28x-24=0
t=2x: t^3+9t^2+14t-24=0(*),
Заметим, что сумма коэффициентов равна нулю, значит есть корень 1.
Поделим многочлен (*) на t-1. Получаем, что
Выходит, что
Значит, ⇒
⇒
⇒
1)
Распределить -2 через скобки:
;
Умножить обе части уравнения на 2:
;
Сложить два уравнения:
3xy=60;
Разделить обе стороны уравнения на 3x:
y=;
Подставить данное значение y в уравнение xy-2x-2y=2:
x·-2x-2·
=2;
Решить уравнение относительно x:
x=5
x=4;
Подставить данное значение x в уравнение 3xy=60:
3·5y=60
3·4y=60;
Решить уравнение относительно y:
y=4
y=5;
Решением системы являются упорядоченные пары (x,y):
(x₁y₁)=(5,4)
(x₂y₂)=(4,5);
Проверка:
;
Упростить уравнения:
;
Упорядоченные пары чисел являются решениями системы уравнений, т.к. равенства истины:
(x₁y₁)=(5,4)
(x₂y₂)=(4,5)
2)
Решить уравнение относительно x:
;
Подставить данное значение x в уравнение 2x³+9xy+25y+44=0:
2(2+y)³+9(2+y)·y+25y+44=0;
Решить уравнение относительно y:
y=
y=-5
y=-4;
Подставить данное значение y в уравнение x=2+y:
x=
x=2-5
x=2-4;
Решить уравнение относительно x:
x=
x=-3
x=-2;
Решениями системы являются упорядоченные пары (x,y):
(x₁y₁)=(,
)
(x₂y₂)=(-3,-5)
(x₃y₃)=(-2,-4);
Проверка:
;
Упростить уравнения:
;
Упорядоченные пары чисел являются решениями системы уравнений, т.к. равенства истины:
(x₁y₁)=(,
)
(x₂y₂)=(-3,-5)
(x₃y₃)=(-2,-4)