Предмет: Алгебра
Автор: zhidelevairina13
Вопрос задан 7 лет назад

< >

Дам 40 баллов!
Помогите пожалуйста, очень-очень нужно!!!!
Прошу Вас!
Нужно решение и ответ

Приложения:

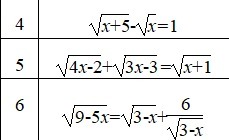
Ответы

Ответ дал: DNHelper

0

4. ОДЗ: x ≥ 0

$sqrt{x+5}=1+sqrt{x}\x+5=1+2sqrt{x}+x\2sqrt{x}=4\sqrt{x}=2\x=4$

Ответ: 4

5. ОДЗ: $begin{equation*} begin{cases} 4x-2geq0, \3x-3geq0,\x+1geq0. end{cases}end{equation*} Rightarrow begin{equation*} begin{cases} xgeqfrac{1}{2},\x geq1,\x geq-1. end{cases}end{equation*} Rightarrow xgeq1$

$4x-2+2sqrt{4x-2}sqrt{3x-1}+3x-3=x+1\2sqrt{4x-2}sqrt{3x-1}=6-6x Rightarrow 6-6xgeq0Rightarrow xleq1Rightarrow x=1$

Проверка:

$sqrt{4-2}+sqrt{3-3}=sqrt{1+1}\sqrt{2}=sqrt{2}$

Верно, корень подходит.

Ответ: 1

6. ОДЗ: $left { {{9-5xgeq0} atop {3-x>0}} right. left { {{xleq1,8} atop {x<3}} right. Rightarrow xleq1,8$

$sqrt{9-5x}= frac{3-x+6}{sqrt{3-x}} \ sqrt{9-5x}sqrt{3-x}=9-x\(9-5x)(3-x)=(9-x)^2\5x^2-24x+27=x^2-18x+81\4x^2-6x-54=0|:2\2x^2-3x-27=0\D=9+4*2*27=225=15^2\x_{1}=frac{3+15}{4}=4,5; x_{2}=frac{3-15}{4}=-3$

x₁ не удовлетворяет ОДЗ.

Ответ: -3

Ответ дал: zhidelevairina13

0

Спасибо большое!! А сможешь еще немножко порешать?

Ответ дал: DNHelper

0

Посмотрю, что можно сделать

Ответ дал: zhidelevairina13

0

https://znanija.com/task/30207124

Похожие вопросы

Другие предметы

2 года назад

Каким духи самых дарагиэ?

Окружающий мир

2 года назад

помогите плиз все задания

Химия

2 года назад

решите пж химия 8 класс сделать превращения ну пожалуйста

Геометрия

2 года назад

стороны параллелограмма равны 2 см, 3 см и 4 см, одна диагональ равна 4 см. Найдите другую диагональ (желательно ответ с рисунком)

Алгебра

8 лет назад

Вычислить..........................................

Математика

8 лет назад

Три мальчика были на рыбалке. Каждый из них поймал по 5 окуней и по 4 карасика. Сколько всего рыбок поймали мальчики? Реши задачу двумя способами. Помогите решить.

Обществознание

9 лет назад

Птицу узнают по полету, а человека по работе. Что это означает? Помогите плиз)))

Литература

9 лет назад

жуковский вопрос. Какое символическое значение имеет море?