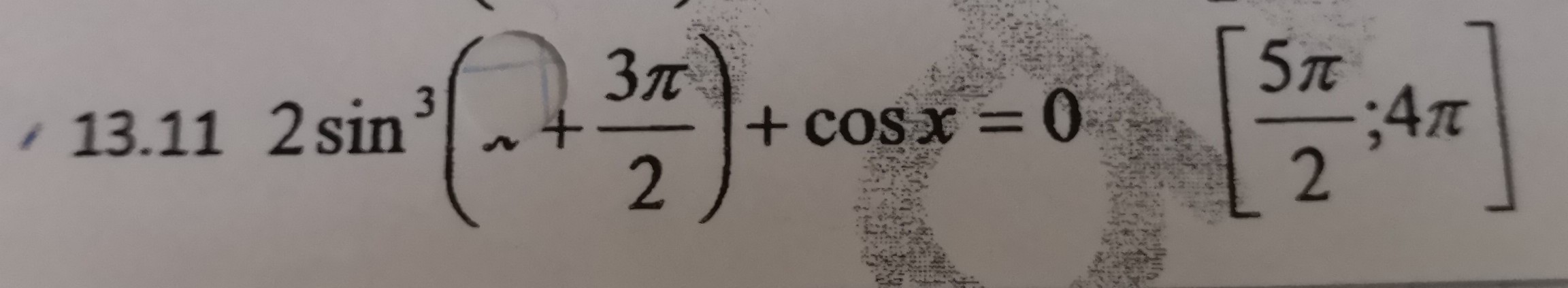Решите тригонометрическое уравнение 13.11

Упростить выражение:

2(-cos(x))³+cos(x)=0;

Отрицательное основание в нечётной степени отрицательно:

2(-cos(x)³)+cos(x)=0;

Произведение положительного и отрицательного значений отрицательно(плюс на минус=минус):

-2cos(x)³+cos(x)=0;

Вынести общий множитель для упрощения вычисления:

-cos(x)·(2cos(x)²-1)=0;

Упростить выражение, используя формулу 2cos(t)²-1=cos(2t):

-cos(x)cos(2x)=0;

Используя формулу cos(2t)=cos(t)²-sin(t)², записать выражение в развёрнутом виде:

-cos(x)(cos(x)²-sin(x)²)=0;

Распределить -cos(x) через скобки:

-cos(x)³+cos(x)sin(x)²=0;

Вынести за скобки общий множитель -cos(x):

-cos(x)(cos(x)²-sin(x)²)=0;

Упростить выражение, используя формулу cos(t)²-sin(t)²=cos(2t):

-cos(x)cos(2x)=0;

Если произведение равно 0,то как минимум один из множителей равен 0:

-cos(x)=0

cos(2x)=0;

Решить уравнение относительно x:

x=,k∈Z

x=,k∈Z;

Ответ:,k∈Z.