Предмет: Математика
Автор: Amilevskay
Вопрос задан 7 лет назад

< >

Вычислить объём тела , образованного вращением вокруг оси Оx кривой L : x^2-y=0 , x=-1, y=0

Ответы

Ответ дал: xxxeol

0

Объем тела вращения по формуле:

$V(x)=pi intlimits^a_b {y^2(x)} , dx= pi intlimits^a_b {x^4} , dx= pi frac{x^5}{5}$

Вычисляем на границах интегрирования - b= -1, a=0

V = π/5 - объем - ОТВЕТ

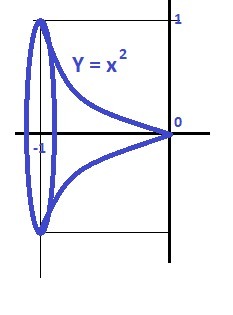
Рисунок ТЕЛА в приложении.

Приложения:

Похожие вопросы

Английский язык

2 года назад

стих перевод с англиского на руски с рождеством

Русский язык

2 года назад

подчеркни безударные гласные. Как называется слова, записанное в скобках? зимой (зимний) ёлка - самое доброе лесное (лес) дерево. Месяцами (месяц) может кормить (корм) она и белку, и дятла, и

Литература

2 года назад

Что такое Каренина ?

Литература

2 года назад

усний твір на тему про що розповідають вірші С.Єсеніна

Алгебра

8 лет назад

Кто может помочь решить интеграл?!

Математика

8 лет назад

Пожалуйста мне нужно срочно это всё решить потому что я на контрольной дам 20 баллов кто решит и Отгадай слово

Математика

9 лет назад

Градусная мера одного из смежных углов равна 200% градусной меры другого. Найдите меньший угол.

Математика

9 лет назад

в гараже стояли машины И мотоциклы у них вместе 56 колёс сколько машин И мотоциклов было,если машин И мотоциклов вместе 18? ПОМОГИТЕ СКАЖИТЕ КАК РЕШИТЬ ДЕЙСТВИЯМИ!!!