Решите уравнения. Сделайте хоть два, остальные я сам попытаюсь поразмыслить!
Заранее спасибо
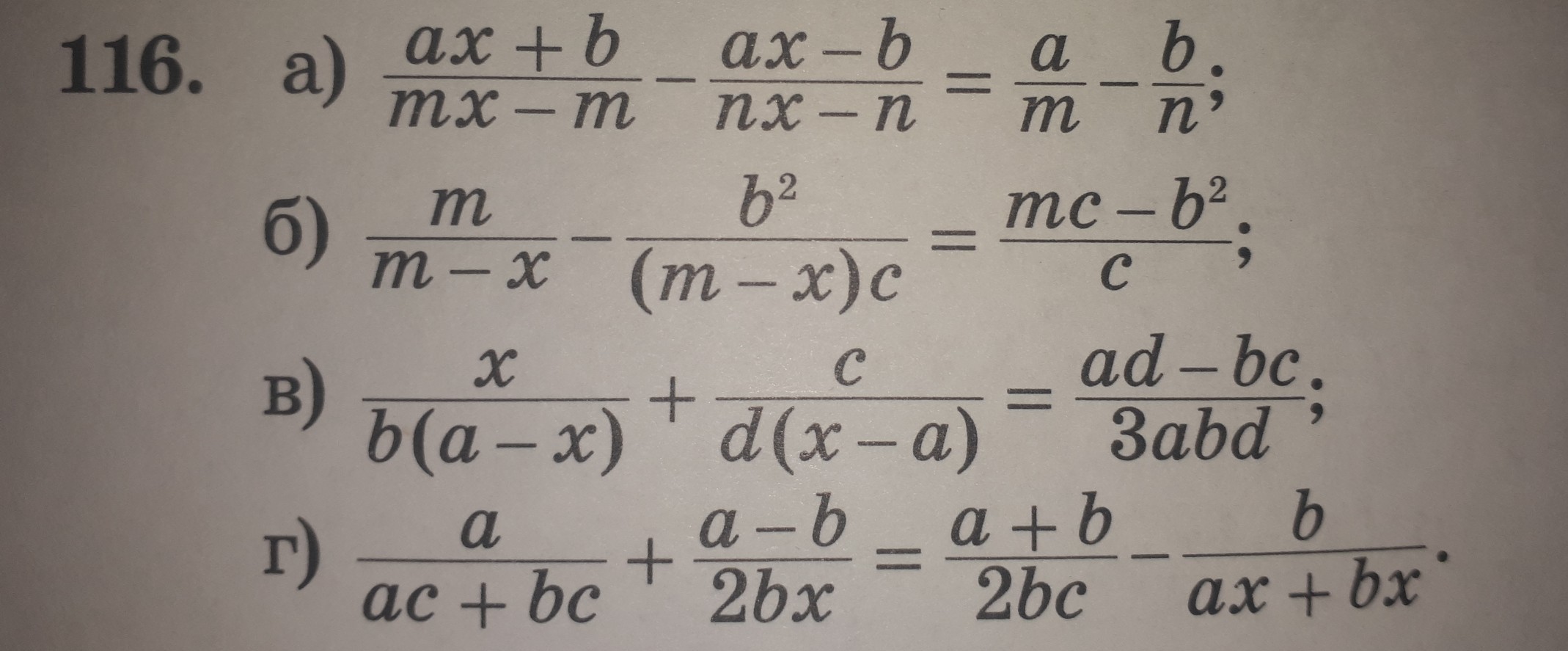
Ответы
а)
Знаменатели все одинаковые, уравниваем числители
n(ax + b) - m(ax - b) = an(x - 1) - bm(x - 1)
anx + bn - amx + mb = anx - an - bmx + bm
Переносим иксы влево, а все остальное вправо.
anx - amx - anx + bmx = bm - an - bn - bm
mx(b - a) = -n(a + b)
При a = b решений нет, при a ≠ b решение:
б)
Знаменатели все одинаковые, уравниваем числители
mc - b^2 = (mc-b^2)(m-x)
При mc = b^2 решений бесконечное множество, x - любое.
При mc ≠ b^2 решение:
m - x = 1; x = m - 1
в)
Знаменатели все одинаковые, уравниваем числители
3adx - 3abc = (ad - bc)(a - x)
3adx - 3abc = a^2*d - abc - adx + bcx
Переносим иксы влево, а все остальное вправо.
4adx - bcx = a^2*d + 2abc
x(4ad - bc) = a(ad + 2bc)
При 4ad = bc решений нет. При 4ad ≠ bc решение:
x = a(ad + 2bc)/(4ad - bc)
г)
Знаменатели все одинаковые, уравниваем числители
2abx + c(a^2 - b^2) = x(a + b)^2 - 2b^2*c
Переносим иксы влево, а все остальное вправо.
2abx - x(a + b)^2 = -a^2*c + b^2*c - 2b^2*c
x(2ab - a^2 - 2ab - b^2) = -c(a^2 + b^2)
-x(a^2 + b^2) = -c(a^2 + b^2)
Если a^2 + b^2 = 0 (то есть a = b = 0), то x - любое
Если a^2 + b^2 ≠ 0, то x = c