Предмет: Алгебра
Автор: BE5Tolo4ь
Вопрос задан 7 лет назад

< >

Найдите все целочисленные решение уравнения
3x^2y^2+4y^2=24x^2+48

Ответы

Ответ дал: Максим757

0

$3 {x}^{2} {y}^{2} + 4 {y}^{2} = 24 {x}^{2} + 48 \ (24 - 3 {y}^{2} ) {x}^{2} = 4 {y}^{2} - 48 \ {x}^{2} = frac{4 {y}^{2} - 48 }{24 - 3 {y}^{2} } = - frac{4( {y}^{2} - 12) }{3( {y}^{2} - 8) } geqslant 0 \ frac{( {y}^{2} - 12) }{( {y}^{2} - 8) } leqslant 0 \ frac{(y -2 sqrt{3})(y + 2 sqrt{3} )}{(y - 2 sqrt{2})(y + 2 sqrt{2} ) } leqslant 0$
Решая (на фото) получаем:
$- 2 sqrt{3} leqslant y < - 2 sqrt{2} : : и : : 2 sqrt{2} < y leqslant 2 sqrt{3}$
Этому условию удовлетворяет только у=-3 и у=3, подставляем:
${x}^{2} = - frac{4( {3}^{2} - 12)}{3( {3}^{2} - 8)} = - frac{4 times ( - 3)}{3 times 1} = 4 \ x = 1 : : или : : x = - 1$
Т. к. у нас у^2, то при у=-3 будут те же корни.

Ответ: (-1;-3); (-1;3); (1;-3); (1;3).

Приложения:

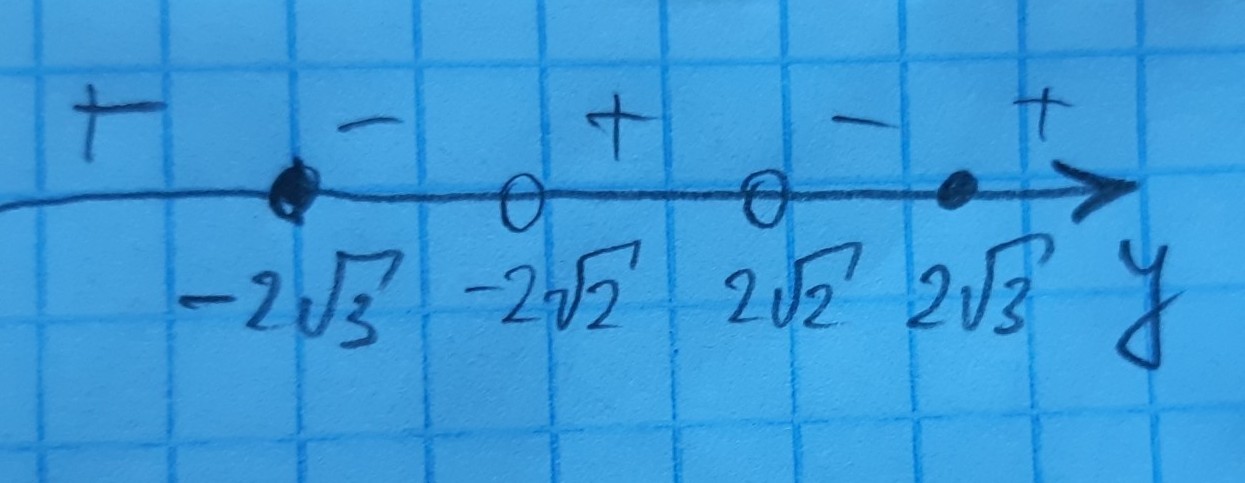
Ответ дал: BE5Tolo4ь

0

Там +4y^2 а не умножить

Ответ дал: BE5Tolo4ь

0

И 24х^2+48

Ответ дал: BE5Tolo4ь

0

Все понял спасибо

Похожие вопросы

Русский язык

2 года назад

мини-сочинение про пословицу с плеча да сгоряча ничего не делай

Английский язык

2 года назад

помагите номер 2, отмечк лучшим

Математика

2 года назад

ПОМОГИТЕ СРОЧНО,НУЖНО РЕШЕНИЕ(ответ должен быть 6 корень из 3).

Алгебра

2 года назад

Сколько будет 285⁶:125⁴×10⁹ Срочно надо пж

Геометрия

8 лет назад

1) А и Б параллельны, они пересечены секущей С, угол 1 больше угла 2 в 2 раза. углы 1 и 2 односторонние, найдите углы 1 и 2. плиз!

Алгебра

8 лет назад

Помогите срочно. Я РЕШЕНИЕ ЗНАЮ МОЖЕТЕ ОБЪЯСНИТЬ ПОЧЕМУ 2 Ч 55 МИН = 35/12 ПОЖАЛУЙСТА водонапорный бак заполняется двумя трубами за 2 часа 55 мин. Первая труба может его наполнить на 2 часа скорее,

Геометрия

9 лет назад

отрезок ab длины a разделен точками P и Q на три отрезка AP , PQ и QB так, что AP= 2PQ=2QB.Найдите расстояние между : а) точкой A и серединой отрезка QB ; б) серединами отрезков AP иQB

Физика

9 лет назад

задания школьного этапа Всероссийской олимпиады школьников по истории 2015 2016 учебный год 11 класса ответы