Привести уравнение кривой второго порядка x^2 + 4y^2 - 4x - 8y - 8 = 0 к каноническому виду. Определить вид кривой, её параметры и сделать рисунок
Ответы
Ответ дал:
0
Выделяем полные квадраты:
для х: (x²-2*2x + 2²) -1*2² = (x-2)²-4
для y: 4(y²-2*y + 1) -4*1 = 4(y-1)²-4
В итоге получаем:
(x-2)²+4(y-1)² = 16
Разделим все выражение на 16 :
((x-2)²)/16) + ((y-1)²)/4 = 1
Полуоси эллипса:
a = 4;b = 2
Данное уравнение определяет эллипс с центром в точке:
C(2; 1)
Найдем координаты фокусов F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами : с = √(16 - 4) = √12 = 2√3.
Приложения:
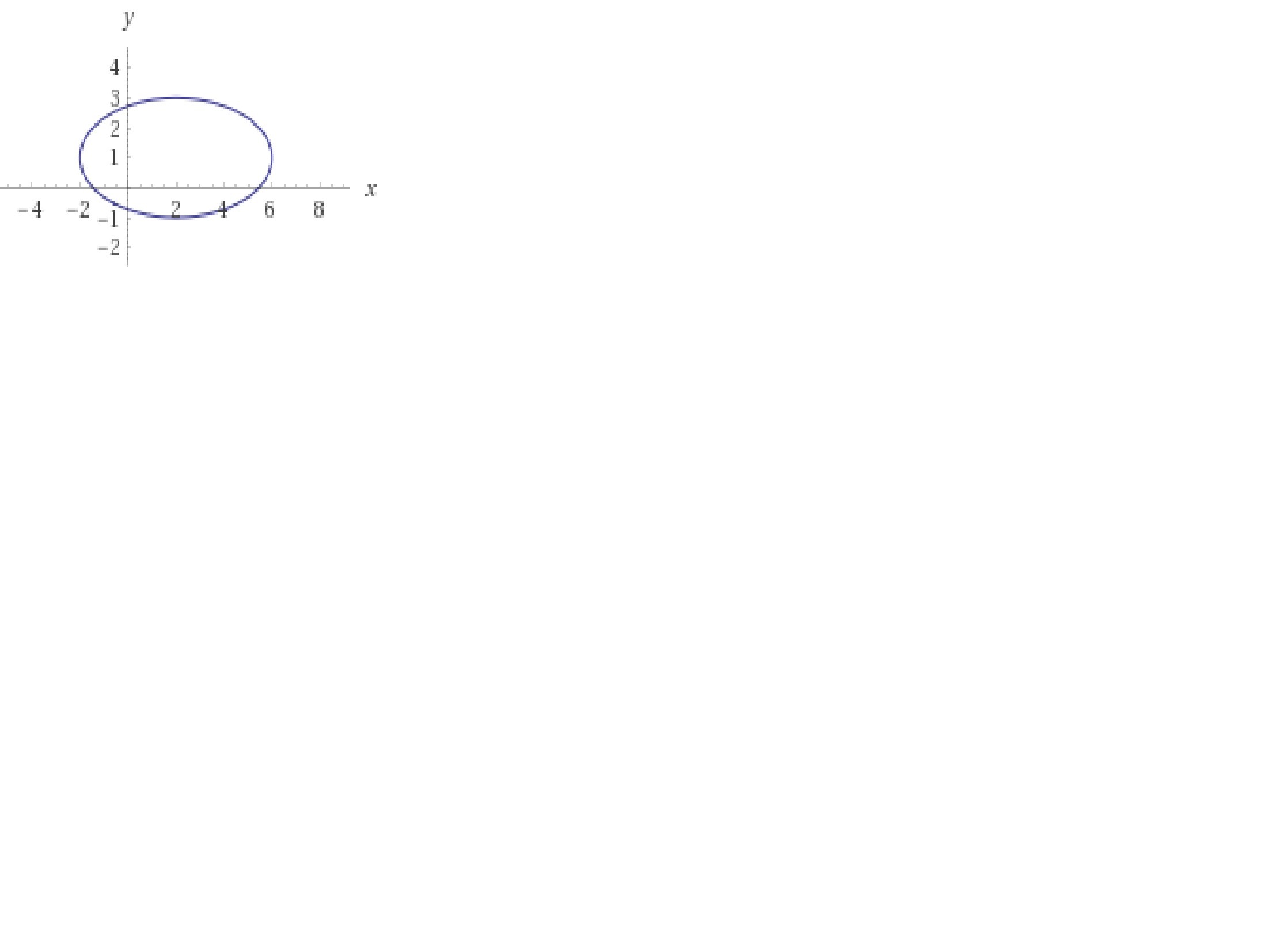
Похожие вопросы
2 года назад
2 года назад
8 лет назад