Ответы
Ответ дал:
0
решение в приложении
Приложения:
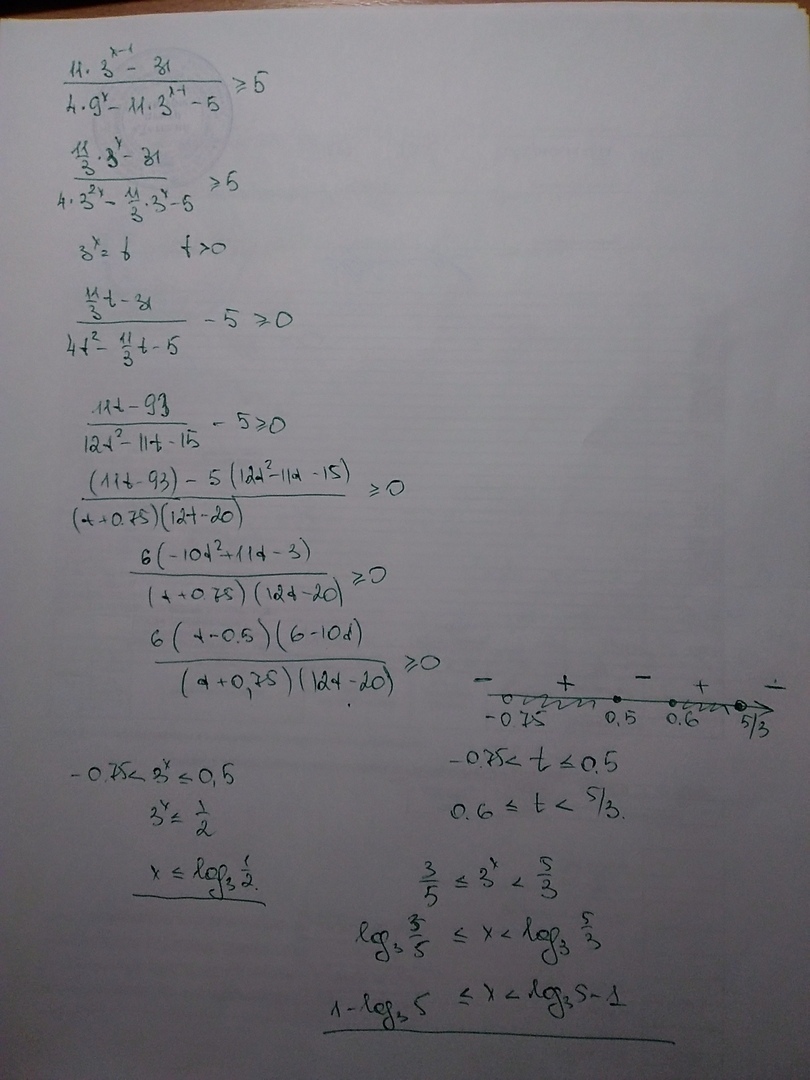

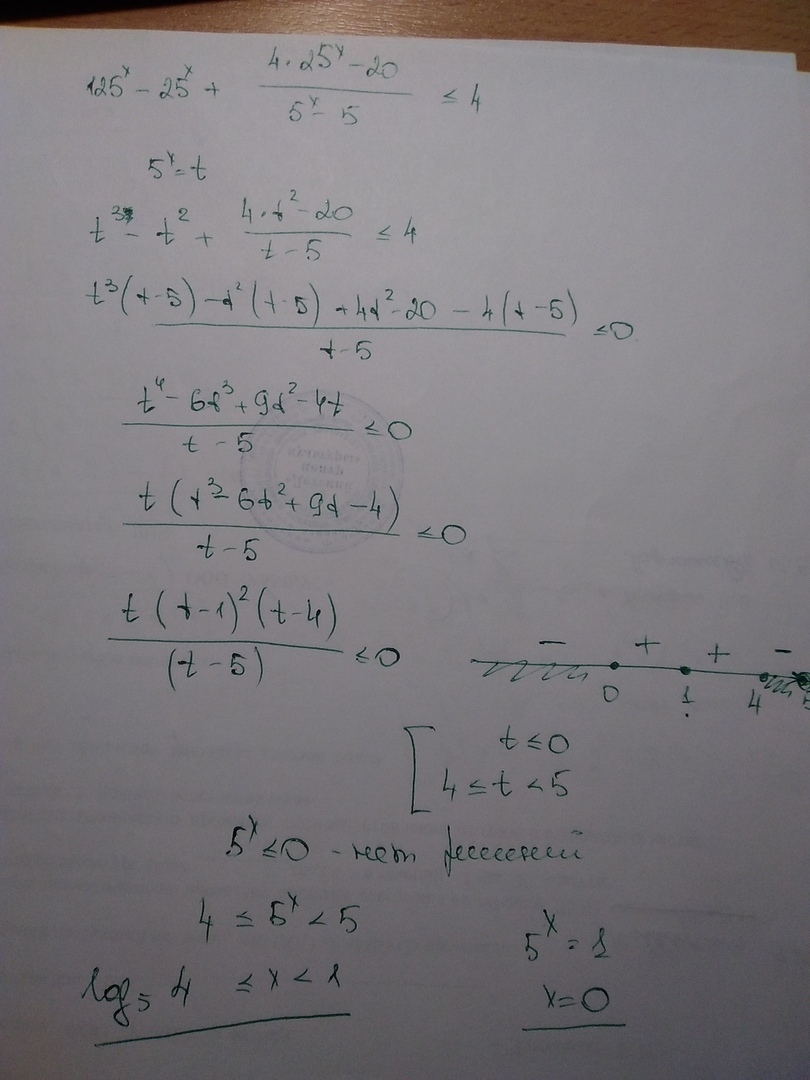
Ответ дал:
0
-180t^2+66t-6=0;
-30t^2+11t-1=0;
D=121-4*30=1;
t=(-11+1)/-60=1/6;
t=(-11-1)/-60=1/5;
___________
36*t^2-11t-5=0;
D=121+4*5*36=841=29²;
t=(11+29)/36=10/9;
t=(11-29)/36=-4/9;∅, т.к. t>0;
+ - + -
___1/6___1/5___10/9___
t ∈ (0;1/6] ∪ [1/5;10/9);
x ∈ (-∞;log₃0,5] ∪ [log₃0,6;log₃10/3);
____________
7)
-2t²+8t-8=0;
D=64-4*2*8=0;
t=-8/-4=2;
_________
2t²-32=0;
t²=16;
t=-4;∅, т.к. t>0;
t=4;
- + -
___2___4___
t ∈ (0;2] ∪ (4;∞);
x ∈ (-∞;1/3] ∪ (2/3;∞);
8)
t-5=0; t₁=5;
t⁴-6t³+9t²-4t=0;
t₂=0;
t³-6t²+9t-4=0;
(t³-4t²)-(2t²-8t)+(t-4)=0;
t²(t-4)-2t(t-4)+(t-4)=0;
(t-4)(t²-2t+1)=0;
t₃=4;
t²-2t+1=0;
(t-1)²=0;
t₄=1;
- + ! + - +
__0___1___4___5___
t ∈ [1] ∪ [4;5);
x ∈ [0] ∪ [log₅4;1);
Приложения:
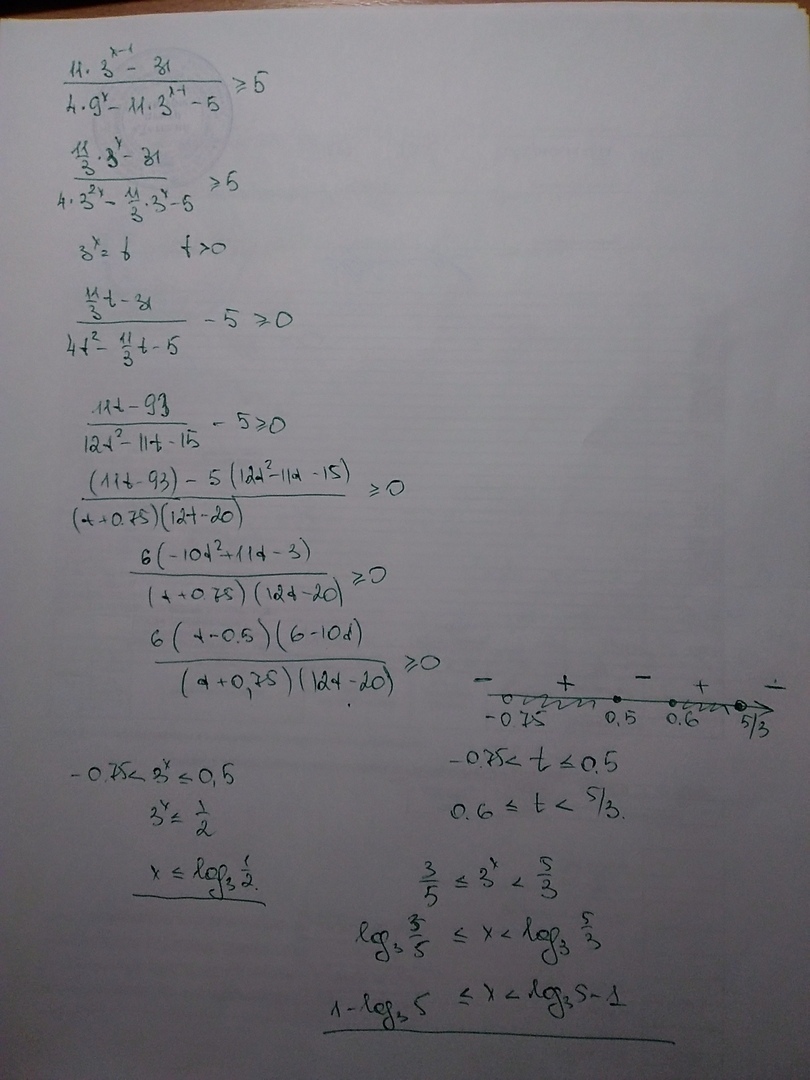

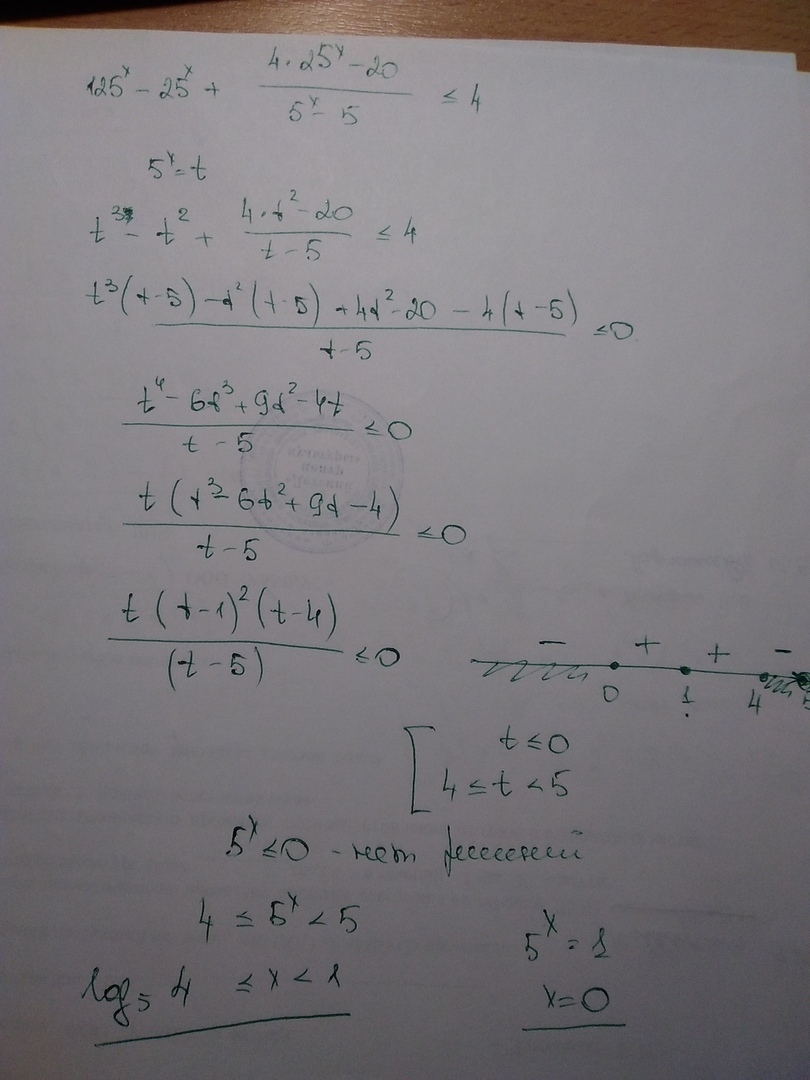
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад
