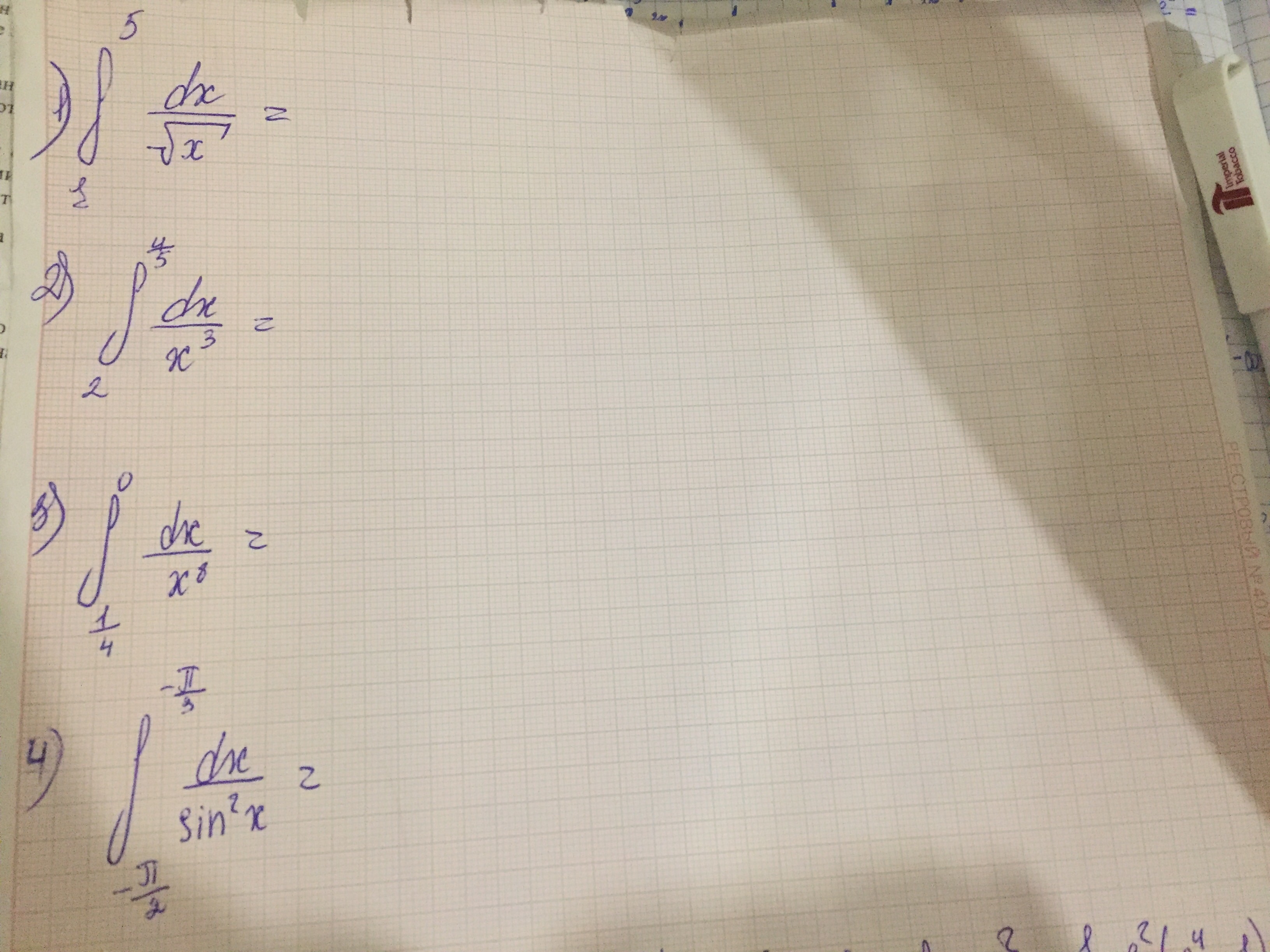Предмет: Алгебра
Автор: mugievaaaaaa
Вопрос задан 7 лет назад

< >

Найдите:
Даю 30 баллов

Приложения:

Ответы

Ответ дал: NNNLLL54

0

$intlimits^5_1, frac{dx}{sqrt{x}}=2sqrt{x}Big |_1^5=2cdot (sqrt5-sqrt1)=2cdot (sqrt5-1)\\intlimits^{4/5}_{2}, frac{dx}{x^3}=frac{x^{-2}}{-2}Big |_2^{4/5}=-frac{1}{2}cdot (frac{1}{frac{16}{25}}-frac{1}{4})=frac{1}{2}cdot (frac{1}{4}-frac{25}{16})=-frac{21}{32}\\intlimits^0_{1/4}, frac{dx}{x^8}=frac{x^{-7}}{-7}Big |_{1/4}^0=-frac{1}{7x^7}Big |^0_{1/4}=?$

Получили, что невозможно подставить предел х=0, т.к. у первообразной переменная $x^7$ стоит в знаменателе, а область определениях функции х≠0. Получаем несобственный интеграл 2 рода.

$intlimits^{-pi /3}_{-pi /2}frac{dx}{sin^2x}=-ctgxBig |_{-pi /2}^{-pi /3}=-(ctg(-frac{pi}{3})-ctg(-frac{pi}{2}))=-(-frac{sqrt3}{3}+0)=frac{sqrt3}{3}$

Ответ дал: Аноним

0

побрей

Ответ дал: Аноним

0

готовься сосать

Ответ дал: Аноним

0

минет сделаеш

Ответ дал: Аноним

0

я тебя жестко трахну

Ответ дал: Аноним

0

готовься лизать минет делать я твою тело трахну

Похожие вопросы

Русский язык

2 года назад

как сделать плизззззз сказите пожалуйста

Русский язык

2 года назад

о чём в слове могут рассказывать полногласные и неполногласные сочетания

Русский язык

2 года назад

Помогите пожайлуста русский язык Срочно !!!!

Русский язык

2 года назад

Плииииз помогите очень надо !!! Даю 20 баллов!!! Спишите, вставляя пропущенные буквы и знаки препинания, подчеркните качественные прилагательные одной чертой, относительные – двумя. 1. Как

Алгебра

8 лет назад

x^2+x-6=0 помогите,подробно.

Биология

8 лет назад

Как рыбы попали в аквариум, что они там едят ?

Алгебра

9 лет назад

туристы на байдарке плыли 2,4 часа по течению реки и 0,8 часов против течения .по течению реки туристы проплыли на 19,2 км больше,чем против течения. найдите скорость байдарки в стоячей воде,если

Алгебра

9 лет назад

Решите, пожалуйста ! $5*(-2)^5$ $-3*(-5)^2$ $- frac{1}{6} * (-3)^3$ $frac{2}{5} * (-2frac{1}{2}) ^3$