На столе стоят песочные часы высоты 16 см, представляющие собой два соединенных усеченных одинаковых конуса. Радиус горлышка (отверстия, через которое сыпется песок) равен 1 см. Тангенс угла раствора конусов равен 4/3. Чему равен объем песочных часов в см3? Ответ округлите до ближайшего целого.

См. прикрепленный файл.

Объем усеченного конуса равен

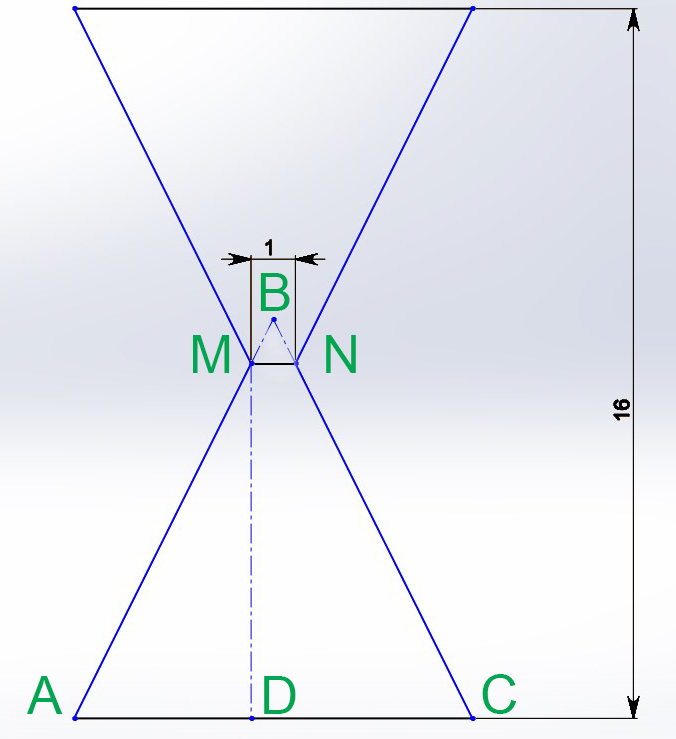
(где h - высота, на рисунке MD=16/2=8 см; r - верхний радиус, на рисунке r=MN/2=1/2=0,5 см, R - радиус основания, на рисунке R=AC/2=?)

ΔАBC равнобедренный (так как конус является фигурой вращения, вокруг центральной оси), значит AM=NC; ∠MAC=∠NCA=° (tg(4/3)≈53°)

⇒ см

R=AD+MN/2=4+0,5=4,5 см

см³

Объем песочных часов будет равен см³