Большая диагональ и большая сторона параллелограмма равны  см и 2 см, а его острый угол стано вить 30 °. Найдите меньшую сторону параллелограмма.

Бóльшая диагональ и бóльшая сторона параллелограмма равны √19 см и 2√3см соответственно, а его острый угол равен 30°. Найти мéньшую сторону параллелограмма. 
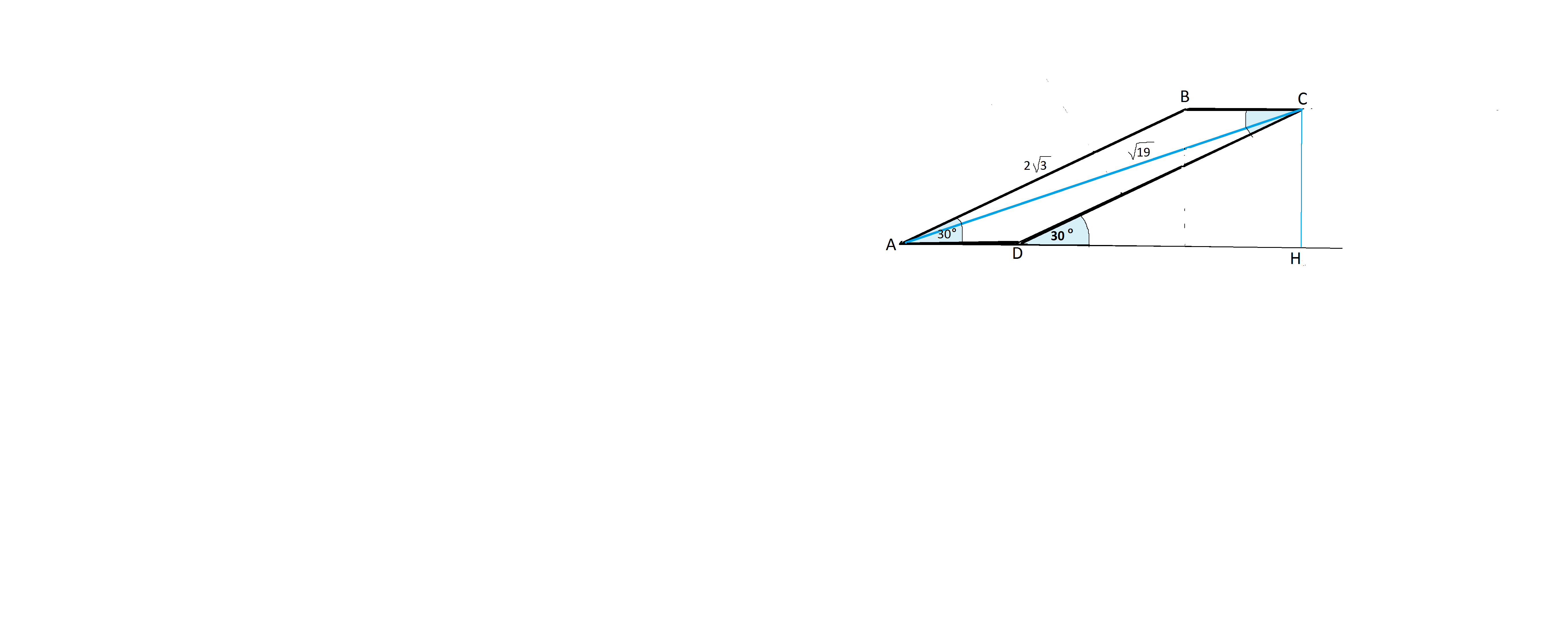
Нарисуем параллелограмм АВСD .  
Опустим из вершины С высоту на прямую АD.
 Поскольку угол А=С=30°, накрестлежащий угол  СDН  в треугольнике СDН  также равен 30°,  и высота СН  будет равна половине большей стороны  СD параллелограмма как катет,  противолежащий углу 30°.
Высота СН равна 0,5*2√3=√3 
ДН равна СD*соsin 30=2√3*√3:2=3 см 
Рассмотрим прямоугольный треугольник АСН 
Гипотенуза АС в нем равна √19, катет  СН= √3 
Применив т. Пифагора, найдем АН = 4см  
АД=АН-DН=1 см