докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости
Ответы
Ответ дал:
0
Расстояние между основаниями в равных трапециях (её высота) одинаково.
Сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°. (Свойство углов при параллельных прямых и секущей)
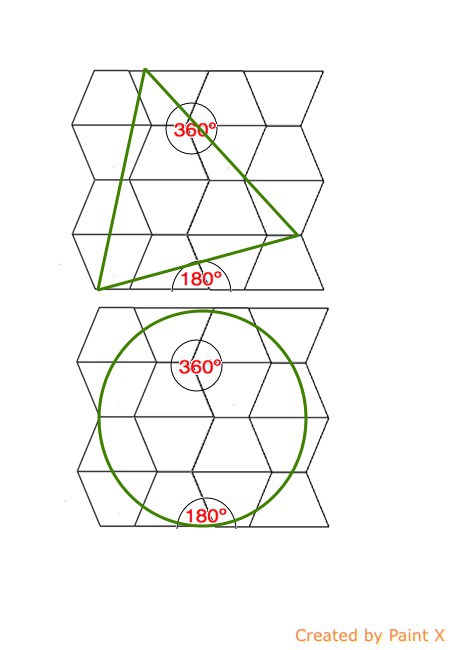
В равнобедренной трапеции углы при её основаниях равны, следовательно, сумма ее противоположных углов также равна 180°. При укладке плитки основаниями на одной линии и боковая сторона к боковой, но с переменой положения оснований, получится единая плоскость без зазоров, которая может покрыть часть плоскости любой формы, что и требовалось доказать. (см. рисунок).
Приложения:
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад