2 Задание желательно расписать , пожалуйста

Приложения:

Ответы

Ответ дал: MaxikMK

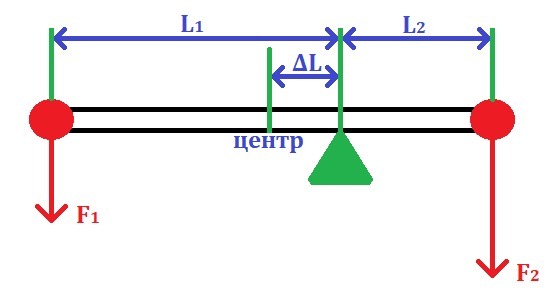
Дано:

Длина стержня: L = 2,5 м.

Масса первого груза: m₁ = 18 кг.

Масса второго груза: m₂ = 54 кг.

Найти расстояние от центра равновесия до центра стержня: ΔL - ?

Решение:

1. Запишем условие равновесия, то есть моменты сил, действующих на стержень: $F_1L_1 = F_2L_2.$

2. Выразим отношение длин: $dfrac{L_2}{L_1} = dfrac{F_1}{F_2}.$

3. Найдём силы тяжести для обоих грузов: $F_1 = m_1g, F_2 = m_2g.$

Физика здесь заканчивается, дальше математика =)

4. Подставим (3) в (2): $dfrac{L_2}{L_1} = dfrac{m_1g}{m_2g} = dfrac{m_1}{m_2}.$

5. Выразим длину второго плеча через длину первого: $L_2 = dfrac{m_1}{m_2}L_1.$

6. Длина всего стержня - сумма длин двух плеч сил, учтём также полученное в (5): $L = L_1 + L_2 = L_1 + dfrac{m_1}{m_2}L_1 = L_1(1 + dfrac{m_1}{m_2}).$

7. Выразим из (6) длину первого плеча: $L_1 = dfrac{L}{(1 + frac{m_1}{m_2})}.$

8. Смотрим на рисунок и видим, что искомая длина — ничто иное, как разность длины большего плеча (очевидно первого, так как масса первого груза меньше ⇒ меньше сила тяжести ⇒ плечо должно быть больше для равновесия) и половины длины стержня: $Delta L = L_1 - dfrac{L}{2} = dfrac{L}{1 + frac{m_1}{m_2}} - dfrac{L}{2} = Lleft(dfrac{1}{1 + frac{m_1}{m_2}} - dfrac{1}{2}right).$