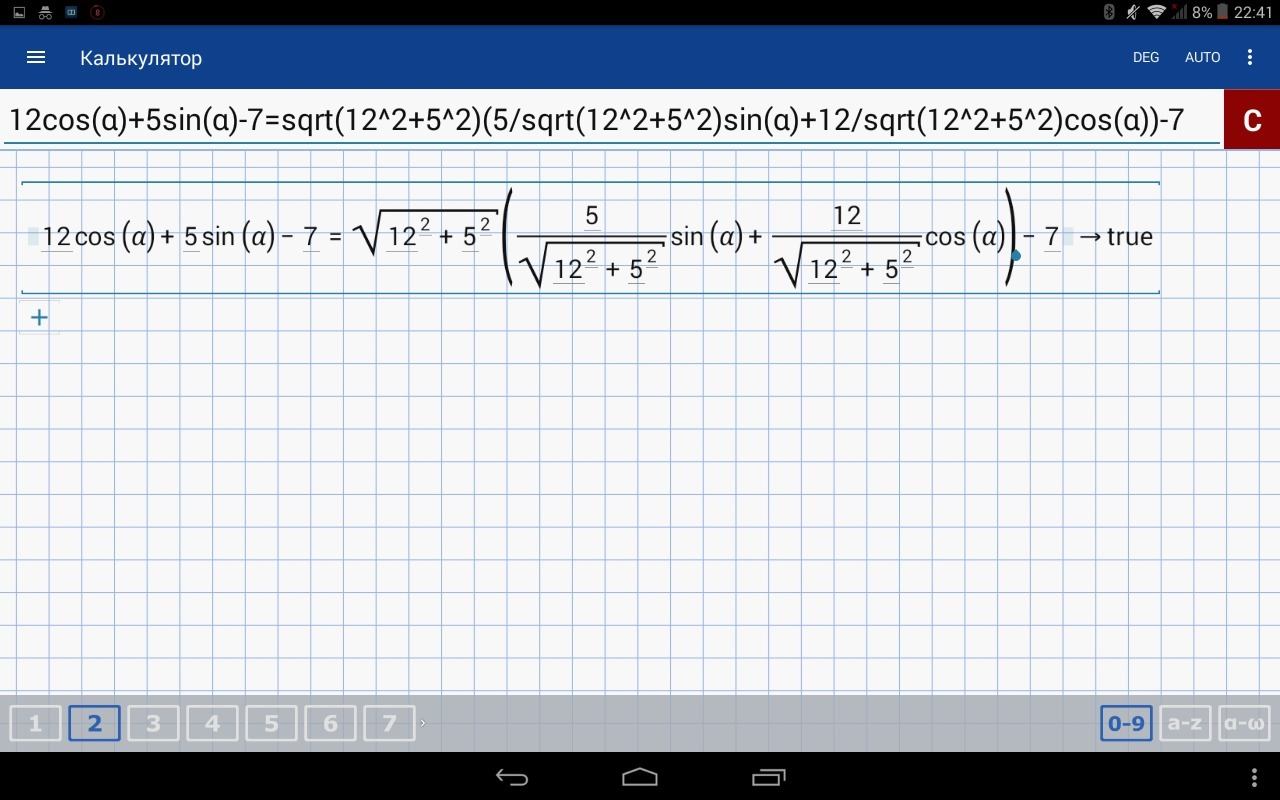
Здраствуйте обясните пожалуйста задачу : найти найбольшее значение у уравнении 12cosA+5sinA-7
Также зачем мы вынесли √(12^2+5^2)
И замем здесь "фи"... : (ф=arccos(5:13)...
Помогите пожалуйста
Приложения:

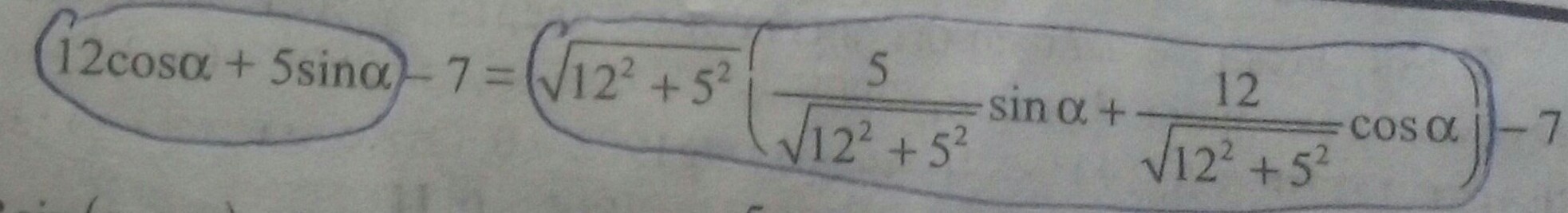
Ответы
Ответ дал:
0
Здесь собственно говоря вам нужно почитать об одной известной формуле: "формула дополнительного угла". Сама формула:
Ваш ответ на вопрос: "Зачем мы вынести √(12^2+5^2)". Это для того, чтобы свести к синусу суммы двух углов, что собственно упростит нам найти наибольшее и наименьшее значения выражения с помощью двойного неравенства.
здесь для простоты обозначили .
Известно, что синус изменяется на промежутке от -1 до 1, и тогда
Откуда наибольшее значение выражения — 6.
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад