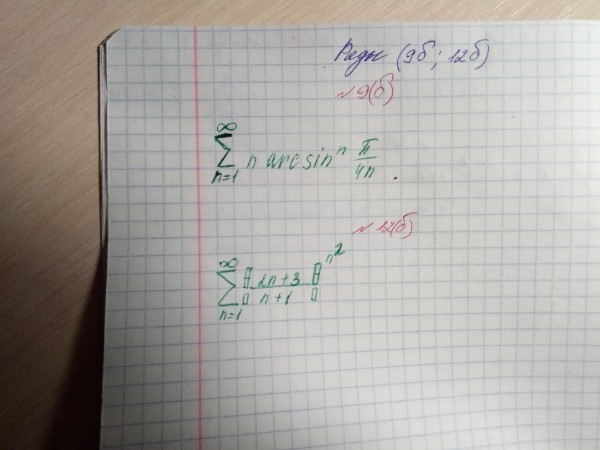Помогите пожалуйста решить ряд

Если требуется исследовать ряды на сходимость, то можно в обоих случаях использовать радикальный признак Коши.

1)

Здесь встретился довольно редко использующийся в учебных заданиях предел . В курсе анализа доказывается, что этот предел равен 1.

Тогда

Предел меньше 1, поэтому ряд сходится.

2)

Ряд расходится.