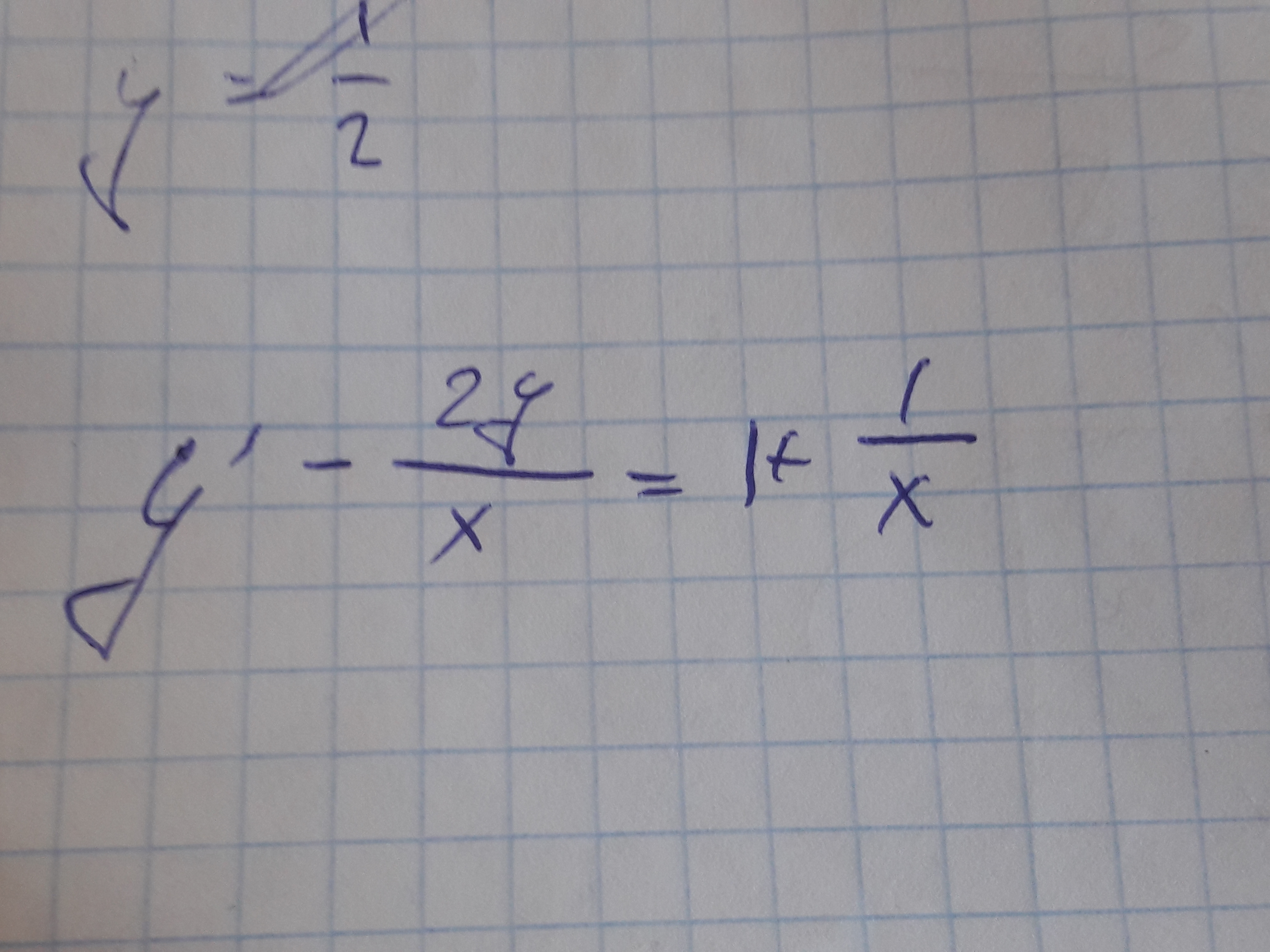Ответы
Ответ дал:
0
У Вас задано линейное неоднородное дифференциальное уравнение. Его можно решать либо методом вариации постоянной, либо подставновкой вида y=u*v. Воспользуемся вторым методом:
Найдём частное решение однородного уравнения, т.е.
Возьмём частное решение при , т.е.
.
Вернёмся к исходному уравнению, и подставим найдённое v:
Тогда, возвращаясь к введённой нами замене, получим:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад