Тело брошено с поверхности земли под углом α = 30° к горизонту со скоростью v₀ = 20 м/с. Пренебрегая сопротивлением воздуха, определите скорость (модуль и направление) и координаты тела через t = 1,5 c после начала движения.
Ответы
Ответ дал:
0
Движение по горизонтали равномерное/
Скорость по горизонтали в любой момент времени равна аналогичной скорости в начале движения.
Движение по вертикали равнопеременное:
Скорость по вертикали уменьшается линейно:
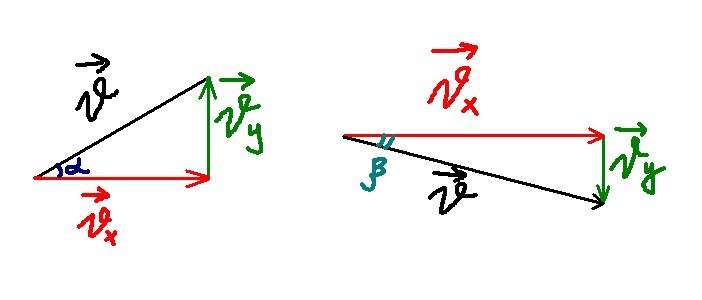
Таким образом, через 1.5 секунды горизонтальная составляющая скорости направлена вправо, а вертикальная - вниз.
Модуль скорости определятся по теореме Пифагора:
Изобразив скорости через 1.5 секунды, определим, что:
, где β - угол между горизонталью и направлением скорости
Ответ: координаты тела х=26м, у=3,75м; скорость равна 18м/с и направлена вниз под углом 16°
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад