Ответы
Ответ дал:
0
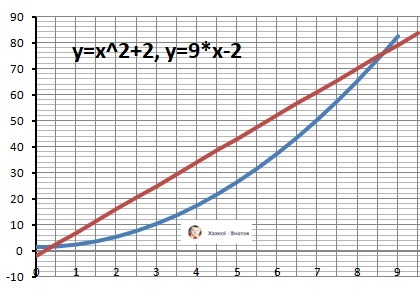
1) Находим пределы интегрирования, решив уравнение
x² + 2 = 9*x - 2 или (прямая выше - находим разность функций)
f(x) = -x² + 9*x - 4 = 0 - это будет подинтегральная функция.
b = 0.47, a = 8.53 - пределы интегрирования
Вычисляем на границах интегрирования.
F(8.53) = -34.125+327.511-206.966 = 86.421
F(0.47) = - 1.875+0.989-0.034 = - 0.921
Площадь - разность интегралов:
F = 86.421 - (-0.921) = 87.341 - площадь фигуры - ОТВЕТ
Приложения:
Ответ дал:
0
вот эти выражения как получились
Ответ дал:
0
я почему то теперь не могу посмотреть ответ помогите что нужно сделать?
Ответ дал:
0
0,47 и 8,53 - корни квадратного уравнения разности функций.
Ответ дал:
0
Я на компе коэффициенты считаю . Проверено.
Ответ дал:
0
И интегралы вычисляем от а и от в и находим разность.
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад