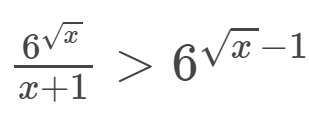Решить неравенство, дробь 6^(sqrtx) / x+1 > 6^(sqrtx)-1

Приложения:

Ответы

Ответ дал: vedma4ka1604

ОДЗ: $xgeq 0, xneq -1$

Прологарифмируем обе части неравенства (с основанием 6):

$log_6(frac{6^{sqrt{x}}}{x+1})>log_6(6^{sqrt{x}-1})\\\log_66^{sqrt{x}}-log_6(x+1)>sqrt{x}-1\\sqrt{x}-log_6(x+1)>sqrt{x}-1\\log_6(x+1)<1\\x+1<6\\x<5$

С учётом ОДЗ в итоге получаем:

$xin[0,5)$

Ответ дал: smayl1ks

"1" не является решением данного неравенства ?

Ответ дал: vedma4ka1604

Ой, простите, конечно же -1, сейчас исправлю

Ответ дал: smayl1ks

Спасибо)

Похожие вопросы

Русский язык

2 года назад

Русский язык

2 года назад

Геометрия

2 года назад

Математика

2 года назад

География

8 лет назад

Математика

8 лет назад

Математика

9 лет назад

Химия

9 лет назад