Предмет: Математика
Автор: ksunya20141485
Вопрос задан 7 лет назад

< >

Предположим что производится обработка стада животных дез составом против заболевания А, вероятность события-заболевания ликвидировано= 0,85. Из стада после обработки отбирается 5 животных, требуется:

1)составить закон распределения числа здоровых животных среди n отобранных
2)А-среди 5 животных будет не более 3 животных, В- не менее 5 здоровых, С- от 3 до 4(включительно)здоровых
3) сколько здоровых животных вероятнее всего будет среди 5 отобранных
4)М(х), Д(х)

Прошу, помогите

Ответы

Ответ дал: Аноним

0

Ответ:

Пошаговое объяснение:

1) Составим закон распределения случайной величины X

$P_5(0)=(1-p)^5=0.85^5\ P_5(1)=C^1_5p(1-p)^4=5times 0.85times 0.15^4=0.00215\ P_5(2)=C^2_5p^2(1-p)^3=dfrac{5!}{2!3!}times0.85^2times 0.15^3=0.024\ P_5(3)=C^3_5p^3(1-p)^2=dfrac{5!}{3!2!}times0.85^3times 0.15^2=0.14\ P_5(4)=C^4_5p^4(1-p)=5times0.85^4times 0.15=0.39\ P_5(5)=p^5=0.85^5=0.44$

2) A — среди 5 животных будет не более 3 здоровых животных

$P(A)=P(kleqslant 3)=1-P(k>3)=1-C^4_5p^4(1-p)-p^5=0.16479$

B — среди 5 животных не менее 5 здоровых животных

$P(B)=P(kgeqslant5)=p^5=0.44$

C — среди 5 животных не менее 3 и не более 4 здоровых

$P(C)=P(3leqslant kleqslant 4)=P_5(3)+P_5(4)=0.14+0.39=0.53$

3) Наивероятнейшее число k определим из двойного неравенства

$np-qleqslant kleqslant np+p\ 5times 0.85-0.15leqslant kleqslant50times0.85+0.85\ 4.1leqslant kleqslant5.1\ k=5$

5 здоровых животных вероятнее всего будет среди 5 отобранных.

4) $M(X)= np = 5times0.85 = 4.25;~~~ D(X)=npq=5times0.85times 0.15=0.6375$

Приложения:

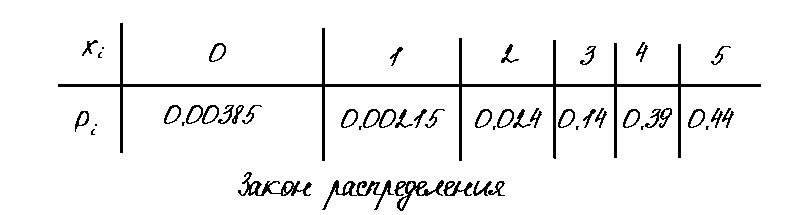
Ответ дал: ksunya20141485

0

Спасибо большое)))

Похожие вопросы

Другие предметы

2 года назад

Сколько нужно выпить воды, чтобы стать тупей на 4.432552%?

Окружающий мир

2 года назад

По своим наблюдениям а также с помощью карты края и материалов по краеведенею назови и опиши основные формы земной поверхности своего края.

Физика

2 года назад

7 10. Четыре черепахи находятся в вер- шинах квадрата со стороной 5,0 м. Черепахи одновременно начинают дви- гаться с одинаковыми по модулю скоро- стями V так, что вектор скорости первой черепахи все

Қазақ тiлi

2 года назад

помогите казахский язык пжж. 4-тапсырма. Артық сөзді сызып, себебін түсіндіріндер. Үлгі: сатып алушы, етікші, адам. Себебі "адам" бұл қаңтардағы жалғыз негізгі түбір сөз. А) Жақсылық, бақыт, өмір,

География

8 лет назад

Ответьте на вопрос: почему у Незнайки на носу выросла большая сосулька, когда он поднимался вверх на воздушном шаре.

Химия

8 лет назад

написать ривняня реакцый H2SO4+CaO=

Математика

9 лет назад

как найти площадь четырехугольника со взаимно перпендикулярными диагоналями размеры:18, 14, 10, 7. Проверить, что площадь такого четырехугольника равна половине произведения диагоналей.

Алгебра

9 лет назад

в магазине продавалось в 3 раза больше коробок машинок, чем в ларьке. когда из магазина привезли 8 коробок машинок в ларек, то их стало поровну. я решила, но хз как правильно 3х-8=х+8 или