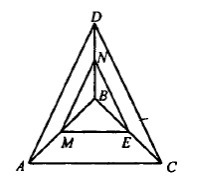
В тетраэдре DABC DA=DC=13, AC=10, E - середина BC. Постройте сечение тетраэдра плоскостью, проходящей через точку Е параллельно плоскости ADC, и найдите площадь сечения.
Ответы
Ответ дал:
0
Дано: DA = DC = 13 , AC = 10 , BE = ЕС , (EMN) II (ADC)
Найти: S(EMN)
Решение:
ME II AC и BE = EC ⇒ ME = AC
MN = NE = AD ⇒ ME = 5
MN = NE =
Выстоа NK , значит медиана ΔMNE ⇒ NK = =
= 6
S(MNE) = · 6 · 5 = 15
Ответ: 15
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад